题目内容
(本题满分12分)在数列 中,
中, ,
, ,
, .
.
(1)证明数列 是等比数列;
是等比数列;
(2)设数列 的前
的前 项和
项和 ,求
,求 的最大值。
的最大值。
 中,
中, ,
, ,
, .
.(1)证明数列
 是等比数列;
是等比数列; (2)设数列
 的前
的前 项和
项和 ,求
,求 的最大值。
的最大值。(1)由题设 ,
,
得 ,
, .又
.又 ,
,
所以数列 是首项为
是首项为 ,且公比为
,且公比为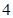 的等比数列;(2)0.
的等比数列;(2)0.
 ,
,得
 ,
, .又
.又 ,
,所以数列
 是首项为
是首项为 ,且公比为
,且公比为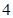 的等比数列;(2)0.
的等比数列;(2)0.试题分析:(Ⅰ)由题设
 ,
,得
 ,
, .又
.又 ,
,所以数列
 是首项为
是首项为 ,且公比为
,且公比为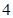 的等比数列.…………4分
的等比数列.…………4分(Ⅱ)由(Ⅰ)可知
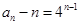 ,于是数列
,于是数列 的通项公式为
的通项公式为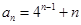 .……………6分
.……………6分所以数列
 的前
的前 项和
项和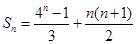 …8分
…8分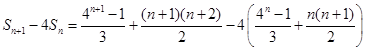
=
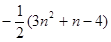 …………………10分
…………………10分故当n=1时,
 的最大值为0. …………………12分
的最大值为0. …………………12分点评:在求数列的通项公式时,常用的一种方法是构造新数列,通过构造的新数列是等差数列或等比数列来求。

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
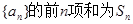 ,
,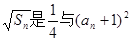 的等比中项。
的等比中项。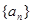 是等差数列;(2)若
是等差数列;(2)若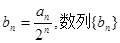 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 的前n项和
的前n项和 满足
满足 (
( >0,且
>0,且 )。数列
)。数列 满足
满足
 的通项。
的通项。 都有
都有 ,求
,求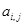 ,且满足
,且满足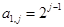 ,
,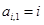 ,
,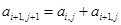 (
(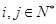 );又记第3行的数3,5,8,13,22,39……为数列{bn},则
);又记第3行的数3,5,8,13,22,39……为数列{bn},则
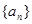 的前
的前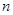 项和为
项和为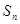 ,已知
,已知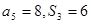 ,则
,则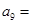 ( )
( )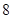
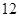
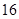
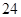
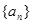 的前n项和为
的前n项和为 ,且
,且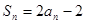 ,(
,( =1,2,3…)
=1,2,3…)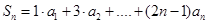 ,求
,求 满足
满足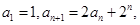 则数列
则数列 项和
项和 = .
= .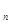 是公差不为0的等差数列
是公差不为0的等差数列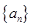 的前n项和,且
的前n项和,且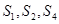 成等比数列。
成等比数列。 ,求
,求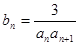 ,
, 是数列
是数列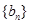 的前n项和,求使得
的前n项和,求使得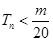 对所有
对所有 都成立的最小正整数
都成立的最小正整数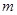 。
。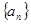 满足
满足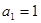 ,且对任意的
,且对任意的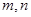
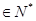 都有:
都有: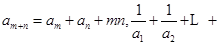
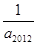 等于 ( )
等于 ( )