题目内容
(本小题满分12分)
数列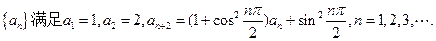
(Ⅰ)求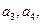 并求数列
并求数列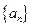 的通项公式;
的通项公式;
(Ⅱ)设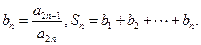 证明:当
证明:当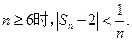
数列
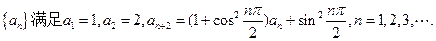
(Ⅰ)求
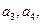 并求数列
并求数列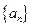 的通项公式;
的通项公式;(Ⅱ)设
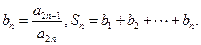 证明:当
证明:当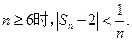
(Ⅰ) 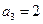 ,
,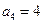 ,
,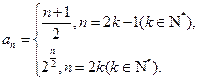 。
。
(Ⅱ)证明见解析。
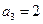 ,
,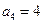 ,
,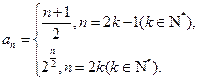 。
。(Ⅱ)证明见解析。
(Ⅰ)因为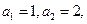 所以
所以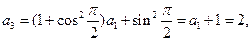
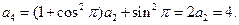
一般地,当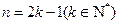 时,
时,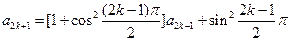
=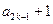 ,即
,即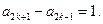
所以数列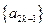 是首项为1、公差为1的等差数列,因此
是首项为1、公差为1的等差数列,因此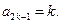
当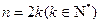 时,
时,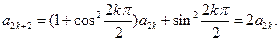
所以数列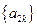 是首项为2、公比为2的等比数列,因此
是首项为2、公比为2的等比数列,因此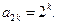
故数列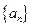 的通项公式为
的通项公式为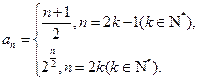
(Ⅱ)由(Ⅰ)知,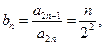
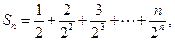 ①
①
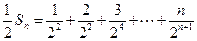 ②
②
①-②得,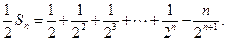
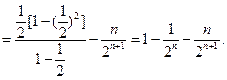
所以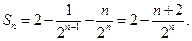
要证明当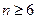 时,
时,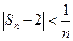 成立,只需证明当
成立,只需证明当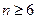 时,
时,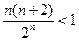 成立.
成立.
证法一
(1)当n = 6时,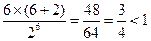 成立.
成立.
(2)假设当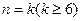 时不等式成立,即
时不等式成立,即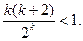
则当n=k+1时,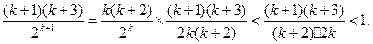
由(1)、(2)所述,当n≥6时, .即当n≥6时,
.即当n≥6时,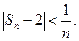
证法二
令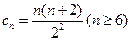 ,则
,则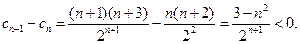
所以当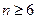 时,
时,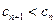 .因此当
.因此当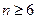 时,
时,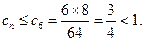
于是当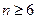 时,
时,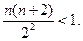
综上所述,当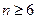 时,
时,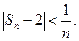
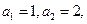 所以
所以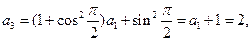
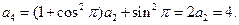
一般地,当
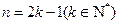 时,
时,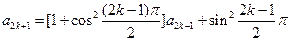
=
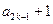 ,即
,即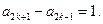
所以数列
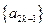 是首项为1、公差为1的等差数列,因此
是首项为1、公差为1的等差数列,因此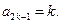
当
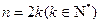 时,
时,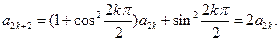
所以数列
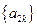 是首项为2、公比为2的等比数列,因此
是首项为2、公比为2的等比数列,因此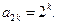
故数列
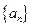 的通项公式为
的通项公式为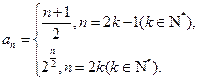
(Ⅱ)由(Ⅰ)知,
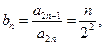
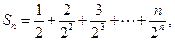 ①
①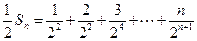 ②
②①-②得,
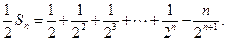
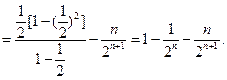
所以
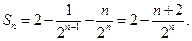
要证明当
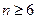 时,
时,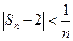 成立,只需证明当
成立,只需证明当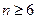 时,
时,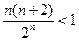 成立.
成立.证法一
(1)当n = 6时,
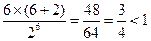 成立.
成立.(2)假设当
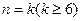 时不等式成立,即
时不等式成立,即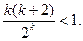
则当n=k+1时,
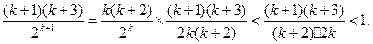
由(1)、(2)所述,当n≥6时,
 .即当n≥6时,
.即当n≥6时,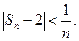
证法二
令
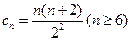 ,则
,则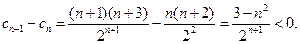
所以当
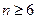 时,
时,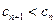 .因此当
.因此当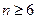 时,
时,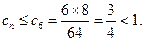
于是当
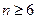 时,
时,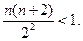
综上所述,当
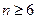 时,
时,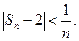

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
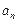 }的公差为d,等比数列{
}的公差为d,等比数列{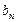 }的公比为q,且,
}的公比为q,且,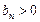 (
(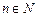 ),若
),若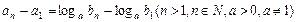 ,求a的取值.
,求a的取值.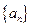 中
中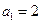 ,
,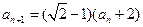 ,
,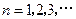 .
.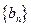 中
中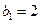 ,
,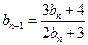 ,
,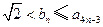 ,
,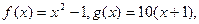 各项均为正数的数列
各项均为正数的数列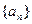 满足
满足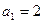 ,
,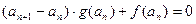 ,
, 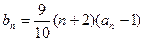 .
. 是等比数列;
是等比数列;  取何值时,
取何值时,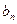 取最大值,并求出最大值;
取最大值,并求出最大值;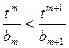 对任意
对任意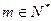 恒成立,求实数
恒成立,求实数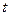 的取值范围.
的取值范围.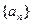 满足
满足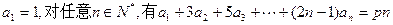 (p为常数)
(p为常数)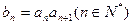 ,求数列
,求数列 的前n项和
的前n项和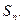
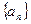 中,
中,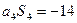 ,
,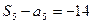 ,其中
,其中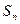 是数列
是数列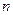 项之和,曲线
项之和,曲线 的方程是
的方程是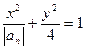 ,直线
,直线 的方程是
的方程是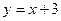 .
.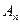 ,
,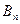 时,令
时,令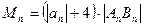 ,
,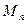 的最小值;
的最小值;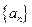 的前n项和
的前n项和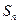 ,
,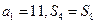 .
.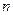 ;(2)求
;(2)求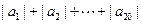 的值.
的值. 为等差数列,
为等差数列, 为其前
为其前 项和
项和
 的反函数为
的反函数为 ,则
,则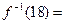 。
。 平面ABC,AB
平面ABC,AB BC,DA=AB=BC=
BC,DA=AB=BC= ,则球O的体积等于 。
,则球O的体积等于 。 (
( ,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的
,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的 ,则此次数学考试成绩不低于110分的学生约有 人。
,则此次数学考试成绩不低于110分的学生约有 人。
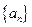 满足
满足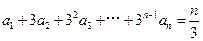 ,
,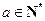 ,则数列
,则数列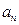 = .
= .