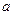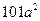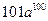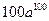题目内容
已知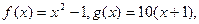 各项均为正数的数列
各项均为正数的数列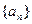 满足
满足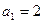 ,
,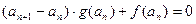 ,
, 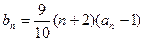 .
.
(Ⅰ)求证:数列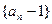 是等比数列;
是等比数列;
(Ⅱ)当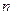 取何值时,
取何值时,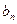 取最大值,并求出最大值;
取最大值,并求出最大值;
(Ⅲ)若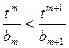 对任意
对任意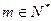 恒成立,求实数
恒成立,求实数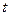 的取值范围.
的取值范围.
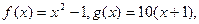 各项均为正数的数列
各项均为正数的数列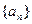 满足
满足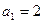 ,
,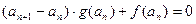 ,
, 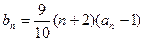 .
.(Ⅰ)求证:数列
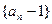 是等比数列;
是等比数列; (Ⅱ)当
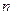 取何值时,
取何值时,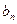 取最大值,并求出最大值;
取最大值,并求出最大值;(Ⅲ)若
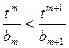 对任意
对任意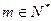 恒成立,求实数
恒成立,求实数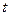 的取值范围.
的取值范围.(I)见解析
(II)当n=7或n=8时,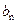 取最大值,最大值为
取最大值,最大值为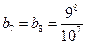 .
.
(III)实数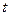 的取值范围是
的取值范围是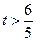
(II)当n=7或n=8时,
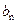 取最大值,最大值为
取最大值,最大值为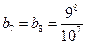 .
.(III)实数
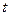 的取值范围是
的取值范围是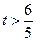
(I)∵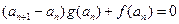 ,
,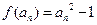 ,
,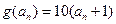 ,
,
∴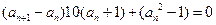 . 即
. 即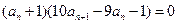 .
.
又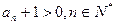 ,所以
,所以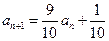 .
.
∵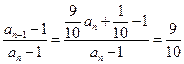 ,
,
∴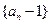 是以
是以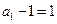 为首项,公比为
为首项,公比为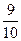 的等比数列.
的等比数列.
(II)由(I)可知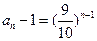 (
( ).
).
∴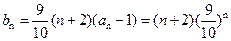 .
.
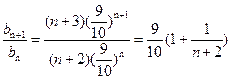 .
.
当n=7时,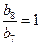 ,
,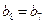 ;
;
当n<7时,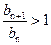 ,
,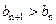 ;
;
当n>7时,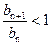 ,
,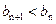 .
.
∴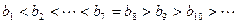
 当n=7或n=8时,
当n=7或n=8时,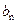 取最大值,最大值为
取最大值,最大值为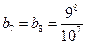 .
.
(III)由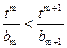 ,得
,得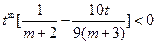 (*)
(*)
依题意(*)式对任意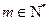 恒成立,
恒成立,
当t=0时,(*)式显然不成立,因此t=0不合题意.
②当t<0时,由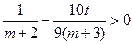 ,可知
,可知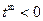 (
(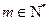 ).
).
而当m是偶数时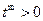 ,因此t<0不合题意.
,因此t<0不合题意.
③当t>0时,由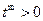 (
(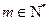 ),
),
∴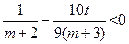 ∴
∴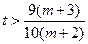 . (
. (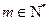 )
)
设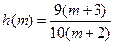 (
(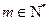 )
)
∵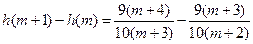 =
=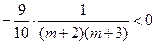 ,
,
∴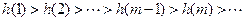 .∴
.∴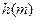 的最大值为
的最大值为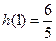 .
.
所以实数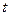 的取值范围是
的取值范围是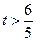 .
.
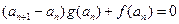 ,
,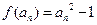 ,
,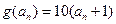 ,
,∴
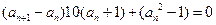 . 即
. 即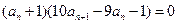 .
.又
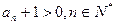 ,所以
,所以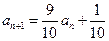 .
.∵
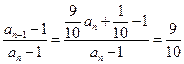 ,
,∴
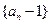 是以
是以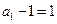 为首项,公比为
为首项,公比为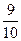 的等比数列.
的等比数列.(II)由(I)可知
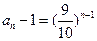 (
( ).
).∴
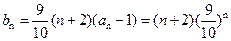 .
.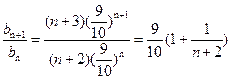 .
.当n=7时,
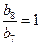 ,
,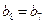 ;
;当n<7时,
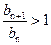 ,
,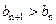 ;
;当n>7时,
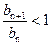 ,
,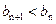 .
.∴
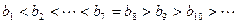
 当n=7或n=8时,
当n=7或n=8时,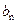 取最大值,最大值为
取最大值,最大值为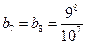 .
.(III)由
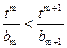 ,得
,得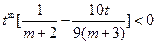 (*)
(*)依题意(*)式对任意
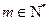 恒成立,
恒成立,当t=0时,(*)式显然不成立,因此t=0不合题意.
②当t<0时,由
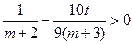 ,可知
,可知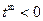 (
(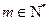 ).
).而当m是偶数时
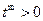 ,因此t<0不合题意.
,因此t<0不合题意.③当t>0时,由
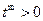 (
(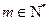 ),
),∴
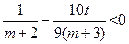 ∴
∴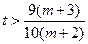 . (
. (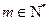 )
)设
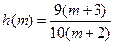 (
(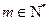 )
)∵
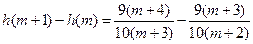 =
=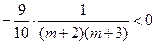 ,
,∴
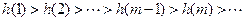 .∴
.∴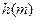 的最大值为
的最大值为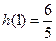 .
.所以实数
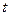 的取值范围是
的取值范围是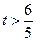 .
.
练习册系列答案
相关题目
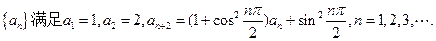
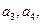 并求数列
并求数列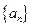 的通项公式;
的通项公式;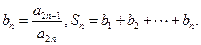 证明:当
证明:当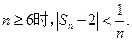
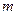 个不全相等的正数
个不全相等的正数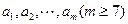 依次围成一个圆圈。
依次围成一个圆圈。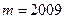 ,且
,且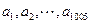 是公差为
是公差为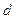 的等差数列,而
的等差数列,而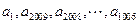 是公比为
是公比为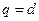 的等比数列;数列
的等比数列;数列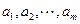 的前
的前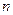 项和
项和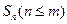 满足:
满足: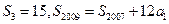 ,求通项
,求通项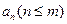 ;
;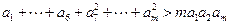 。
。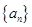 满足
满足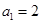 ,
,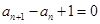
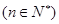 ,则此数列的通项
,则此数列的通项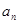 等于
等于 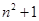
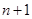

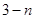
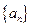 的前三项之积为512,且这三项分别减去1,3,9后又成等差数列,求数列
的前三项之积为512,且这三项分别减去1,3,9后又成等差数列,求数列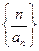 的前n项和
的前n项和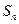 .
.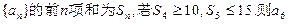 的最大值为 。
的最大值为 。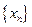 满足
满足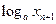 =1+
=1+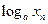 ,且
,且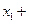
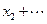
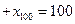 ,则
,则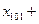
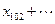 +
+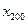 的值为 ( )
的值为 ( )