题目内容
在等差数列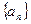 中,
中,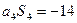 ,
,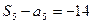 ,其中
,其中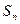 是数列
是数列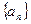 的前
的前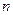 项之和,曲线
项之和,曲线 的方程是
的方程是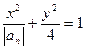 ,直线
,直线 的方程是
的方程是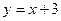 .
.
(1) 求数列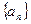 的通项公式;
的通项公式;
(2) 当直线 与曲线
与曲线 相交于不同的两点
相交于不同的两点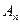 ,
,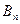 时,令
时,令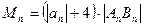 ,
,
求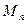 的最小值;
的最小值;
(3) 对于直线 和直线外的一点P,用“
和直线外的一点P,用“ 上的点与点P距离的最小值”定义点P到直线
上的点与点P距离的最小值”定义点P到直线 的距离与原有的点到直线距离的概念是等价的,若曲线
的距离与原有的点到直线距离的概念是等价的,若曲线 与直线
与直线 不相交,试以类似的方式给出一条曲线
不相交,试以类似的方式给出一条曲线 与直线
与直线 间“距离”的定义,并依照给出的定义,在
间“距离”的定义,并依照给出的定义,在 中自行选定一个椭圆,求出该椭圆与直线
中自行选定一个椭圆,求出该椭圆与直线 的“距离”.
的“距离”.
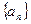 中,
中,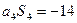 ,
,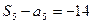 ,其中
,其中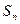 是数列
是数列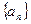 的前
的前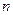 项之和,曲线
项之和,曲线 的方程是
的方程是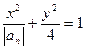 ,直线
,直线 的方程是
的方程是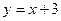 .
.(1) 求数列
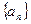 的通项公式;
的通项公式;(2) 当直线
 与曲线
与曲线 相交于不同的两点
相交于不同的两点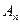 ,
,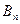 时,令
时,令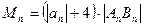 ,
,求
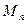 的最小值;
的最小值;(3) 对于直线
 和直线外的一点P,用“
和直线外的一点P,用“ 上的点与点P距离的最小值”定义点P到直线
上的点与点P距离的最小值”定义点P到直线 的距离与原有的点到直线距离的概念是等价的,若曲线
的距离与原有的点到直线距离的概念是等价的,若曲线 与直线
与直线 不相交,试以类似的方式给出一条曲线
不相交,试以类似的方式给出一条曲线 与直线
与直线 间“距离”的定义,并依照给出的定义,在
间“距离”的定义,并依照给出的定义,在 中自行选定一个椭圆,求出该椭圆与直线
中自行选定一个椭圆,求出该椭圆与直线 的“距离”.
的“距离”.(Ⅰ)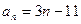 ;(Ⅱ)
;(Ⅱ)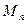 的最小值为
的最小值为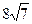 ;(Ⅲ)椭圆
;(Ⅲ)椭圆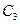 到直线
到直线 的距离为
的距离为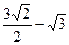 。
。
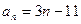 ;(Ⅱ)
;(Ⅱ)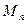 的最小值为
的最小值为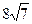 ;(Ⅲ)椭圆
;(Ⅲ)椭圆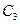 到直线
到直线 的距离为
的距离为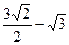 。
。(1)∵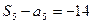 ,∴
,∴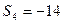 ,又∵
,又∵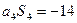 ,∴
,∴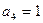 ,
,
∵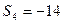
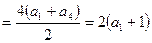 ,
,
∴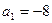 ,
,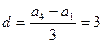 ,
,
∴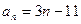 。
。
(2)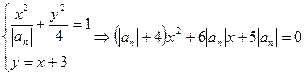 ,由题意,知
,由题意,知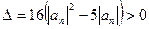 ,即
,即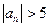 , ∴
, ∴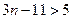 或
或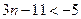 ,即
,即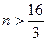 或
或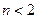 ,
,
即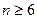 或
或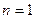 时,直线
时,直线 与曲线
与曲线 相交于不同的两点。
相交于不同的两点。
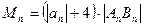
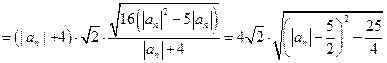
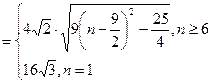 ,
,
∴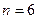 时,
时,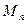 的最小值为
的最小值为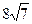 。
。
(3)若曲线 与直线
与直线 不相交,曲线
不相交,曲线 与直线
与直线 间“距离”是:曲线
间“距离”是:曲线 上的点到直线
上的点到直线 距离的最小值。∵曲线
距离的最小值。∵曲线 与直线
与直线 不相交时,
不相交时,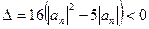 ,即
,即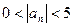 ,即
,即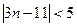 ,∴
,∴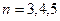 ,
,
∵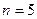 时,曲线
时,曲线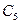 为圆,∴
为圆,∴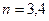 时,曲线
时,曲线 为椭圆。选
为椭圆。选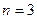 ,
,
椭圆方程为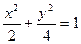 ,
,
设椭圆上任一点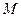
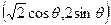 ,它到直线
,它到直线 的距离
的距离
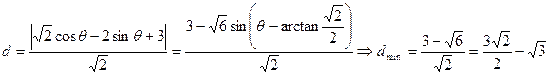
∴椭圆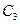 到直线
到直线 的距离为
的距离为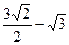 。 (椭圆
。 (椭圆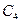 到直线
到直线 的距离为
的距离为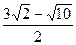 )
)
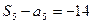 ,∴
,∴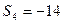 ,又∵
,又∵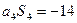 ,∴
,∴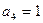 ,
,∵
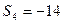
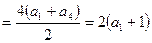 ,
,∴
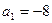 ,
,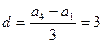 ,
,∴
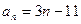 。
。(2)
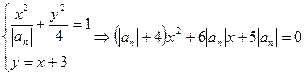 ,由题意,知
,由题意,知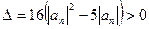 ,即
,即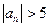 , ∴
, ∴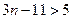 或
或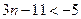 ,即
,即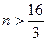 或
或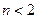 ,
,即
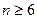 或
或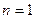 时,直线
时,直线 与曲线
与曲线 相交于不同的两点。
相交于不同的两点。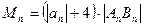
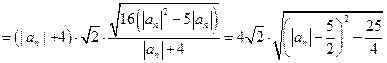
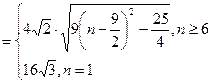 ,
,∴
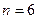 时,
时,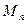 的最小值为
的最小值为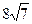 。
。(3)若曲线
 与直线
与直线 不相交,曲线
不相交,曲线 与直线
与直线 间“距离”是:曲线
间“距离”是:曲线 上的点到直线
上的点到直线 距离的最小值。∵曲线
距离的最小值。∵曲线 与直线
与直线 不相交时,
不相交时,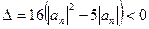 ,即
,即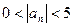 ,即
,即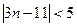 ,∴
,∴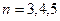 ,
,∵
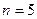 时,曲线
时,曲线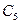 为圆,∴
为圆,∴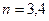 时,曲线
时,曲线 为椭圆。选
为椭圆。选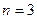 ,
,椭圆方程为
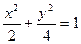 ,
,设椭圆上任一点
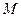
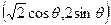 ,它到直线
,它到直线 的距离
的距离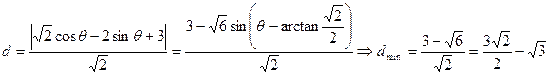
∴椭圆
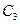 到直线
到直线 的距离为
的距离为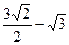 。 (椭圆
。 (椭圆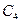 到直线
到直线 的距离为
的距离为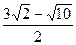 )
)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
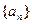 中,
中,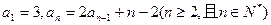
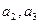 的值;
的值;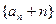 是等比数列,并求
是等比数列,并求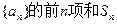 。
。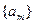 是首项为,公差为
是首项为,公差为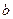 的等差数列,
的等差数列,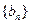 是首项为
是首项为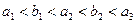 ,其中
,其中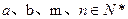 .
.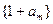 与数列
与数列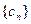 ,求数列
,求数列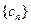 的通项公式;
的通项公式;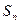 ,求证:
,求证: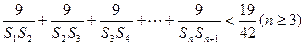 .
.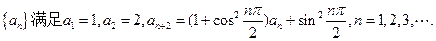
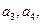 并求数列
并求数列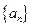 的通项公式;
的通项公式;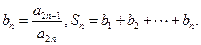 证明:当
证明:当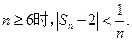
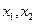 (
(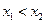 )是方程
)是方程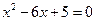 的两根,且
的两根,且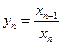 ,
,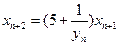 .
. 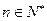 (1)求
(1)求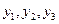 的值;(2)设
的值;(2)设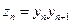 ,求证:
,求证: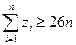 ;(3)求证:对
;(3)求证:对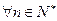 有
有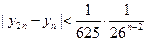 w。.w..
w。.w..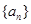 的前
的前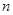 项的和
项的和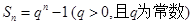 ,某同学得出如下三个结论:①
,某同学得出如下三个结论:①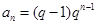 ;②
;②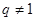 时,
时,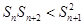 ,
,
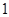
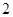
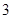
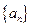 的前三项之积为512,且这三项分别减去1,3,9后又成等差数列,求数列
的前三项之积为512,且这三项分别减去1,3,9后又成等差数列,求数列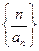 的前n项和
的前n项和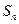 .
.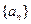 的前
的前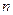 项和
项和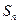 ,且
,且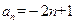 ,则数列
,则数列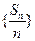 的前11项和为
的前11项和为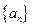 和
和 的前n项和分别为
的前n项和分别为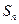 和
和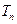 ,若对一切正整数n都有
,若对一切正整数n都有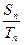 =
=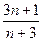 ,则
,则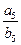 的值为 .
的值为 .