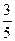题目内容
.(本小题满分14分)
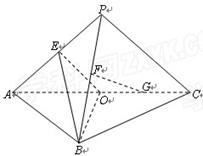
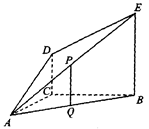
如图,平面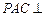 平面
平面 ,点E、F、O分别为线段PA、PB、AC的中点,点
,点E、F、O分别为线段PA、PB、AC的中点,点 G是线段
G是线段 CO的中点,
CO的中点,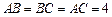 ,
,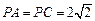 .求证:
.求证:
(1)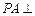 平面
平面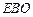 ;
;
(2)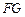 ∥平面
∥平面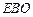 .
.
如图,平面
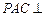 平面
平面 ,点E、F、O分别为线段PA、PB、AC的中点,点
,点E、F、O分别为线段PA、PB、AC的中点,点 G是线段
G是线段 CO的中点,
CO的中点,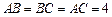 ,
,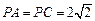 .求证:
.求证:
(1)
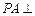 平面
平面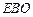 ;
;(2)
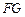 ∥平面
∥平面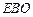 .
.由题意可知,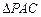 为等腰直角三角形,
为等腰直角三角形,
 为等边三角形. …………………2分
为等边三角形. …………………2分
(1)因为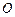 为边
为边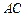 的中点,所以
的中点,所以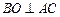 ,
,
因为平面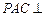 平面
平面 ,平面
,平面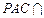 平面
平面 ,
,
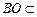 平面
平面 ,所以
,所以 面
面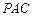 .…………………5分
.…………………5分
因为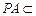 平面
平面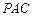 ,所以
,所以 ,
,
在等腰三角形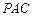 内,
内,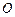 ,
,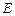 为所在边的中点,所以
为所在边的中点,所以 ,
,
又 ,所以
,所以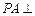 平面
平面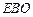 ;…………………8分
;…………………8分
(2)连AF交BE于Q,连QO.

因为E、F、O分别为边PA、PB、PC的中点,
所以 ,且Q是△PAB的重心,…………………10分
,且Q是△PAB的重心,…………………10分
于是 ,所以FG//QO. …………………12分
,所以FG//QO. …………………12分
因为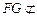 平面EBO,
平面EBO,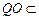 平面EBO,所以
平面EBO,所以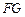 ∥平面
∥平面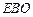 . …………14分
. …………14分
【注】第(2)小题亦可通过取PE中点H,利用平面FGH//平面EBO证得.
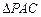 为等腰直角三角形,
为等腰直角三角形, 为等边三角形. …………………2分
为等边三角形. …………………2分(1)因为
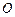 为边
为边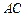 的中点,所以
的中点,所以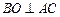 ,
,因为平面
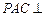 平面
平面 ,平面
,平面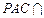 平面
平面 ,
,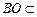 平面
平面 ,所以
,所以 面
面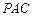 .…………………5分
.…………………5分因为
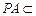 平面
平面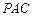 ,所以
,所以 ,
,在等腰三角形
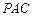 内,
内,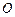 ,
,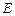 为所在边的中点,所以
为所在边的中点,所以 ,
,又
 ,所以
,所以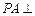 平面
平面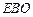 ;…………………8分
;…………………8分(2)连AF交BE于Q,连QO.

因为E、F、O分别为边PA、PB、PC的中点,
所以
 ,且Q是△PAB的重心,…………………10分
,且Q是△PAB的重心,…………………10分于是
 ,所以FG//QO. …………………12分
,所以FG//QO. …………………12分因为
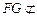 平面EBO,
平面EBO,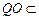 平面EBO,所以
平面EBO,所以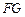 ∥平面
∥平面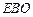 . …………14分
. …………14分【注】第(2)小题亦可通过取PE中点H,利用平面FGH//平面EBO证得.
略

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 ,
,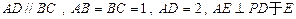 ,
, 。
。
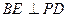 ;
; ;
;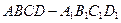 中,
中,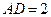 ,
,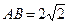 ,
,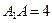 ,
,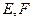 分别是
分别是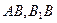 的中点.
的中点.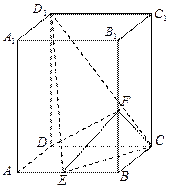
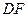 ⊥平面
⊥平面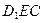 ;
;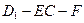 的大小.
的大小. ,四棱锥
,四棱锥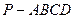 的底面是边长为
的底面是边长为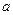 的菱形,
的菱形,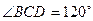 ,
,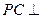 平面
平面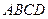 ,
,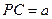 ,
,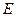 为
为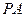 的中点,O为底面对角线的交点;
的中点,O为底面对角线的交点;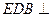 平面
平面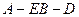 的正切值。
的正切值。
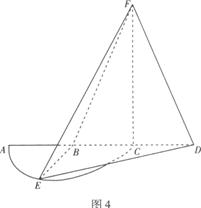
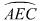 是半径为
是半径为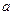 的半
的半 圆,
圆,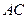 为直径,点
为直径,点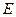 为
为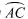 的中点,点
的中点,点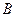 和点
和点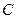 为线段
为线段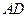 的三等分点,平面
的三等分点,平面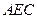 外一点
外一点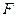 满足
满足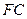
 平面
平面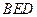 ,
,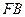 =
=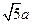 .
. 
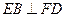 ;
;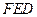 的距离.
的距离. 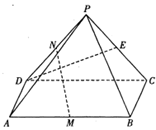
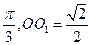 ,则
,则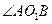 =( )
=( )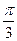 B.
B.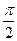 C.
C.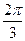 D.
D.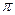
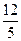 B
B
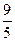 C.
C. D.
D.