题目内容
三棱锥S—ABC中,SA⊥底面ABC,SA=4,AB=3,D为AB的中点∠ABC=90°,则点D到面SBC的距离等于
A.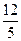 B
B
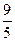 C.
C.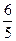 D.
D.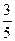
A.
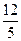 B
B
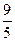 C.
C.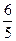 D.
D.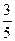
C
略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
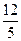 B
B
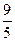 C.
C.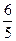 D.
D.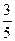

 名校课堂系列答案
名校课堂系列答案