题目内容
((本小题满分12分)
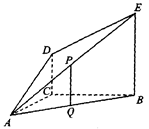
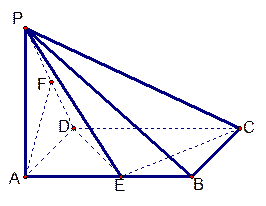
如图,DC⊥平面ABC,EB // DC,AC =BC = EB = 2DC=2,∠ACB=120°,
P,Q分别为AE,AB的中点。
(1)证明:PQ //平面ACD;
(2)求AD与平面ABE所成角的正弦值。

如图,DC⊥平面ABC,EB // DC,AC =BC = EB = 2DC=2,∠ACB=120°,
P,Q分别为AE,AB的中点。
(1)证明:PQ //平面ACD;
(2)求AD与平面ABE所成角的正弦值。
|
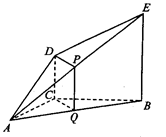 解:(1)因为P,Q分别为 AE,AB的中点,
解:(1)因为P,Q分别为 AE,AB的中点,所以PQ//EB.又DC//EB,因此PQ//DC,
从而PQ//平面ACD.………………………………5分
(2)如图,连接CQ, DP.
因为Q为AB的中点,且AC
 =BC,所以CQ⊥ AB.
=BC,所以CQ⊥ AB.因为DC⊥ 平面ABC,EB//DC,
所以EB⊥ 平面ABC.
因此CQ⊥ EB
故CQ⊥ 平面ABE.
由(1)有PQ//DC,又PQ=
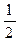 EB=DC,
EB=DC,所以四边形CQPD为平行四边形,
故DP// CQ ,
因此DP ⊥平面ABE,∠ DAP为AD和平面ABE所成的角.
在Rt ∆DPA中,AD=
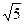 ,DP=1,
,DP=1,sin ∠ DAP=
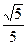
因此AD和平面ABE所成角的的正弦值为
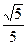 ………………12分
………………12分略

练习册系列答案
相关题目
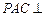 平面
平面 ,点E、F、O分别为线段PA、PB、AC的中点,点
,点E、F、O分别为线段PA、PB、AC的中点,点 G是线段
G是线段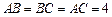 ,
,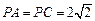 .求证:
.求证: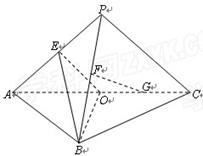
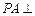 平面
平面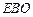 ;
;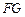 ∥平面
∥平面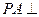 平面
平面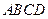 ,底面
,底面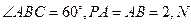 为
为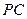 的中点.
的中点.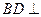 平面
平面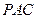 ;
;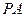 //平面
//平面 ;
; 的平面角的大小.
的平面角的大小.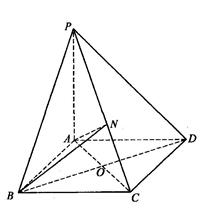
 中,
中, ,
,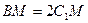
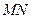 的长度。(12分)
的长度。(12分)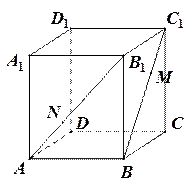
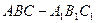 ,底面三角形
,底面三角形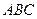 为正三角形,侧棱
为正三角形,侧棱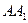
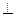 底面
底面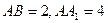 ,
,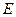 为
为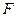 为
为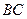 中点.
中点.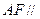 平面
平面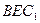 ;
;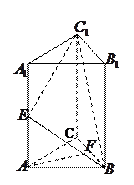
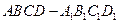 中,异面直线
中,异面直线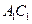 与
与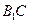 的夹角的大小为__________
的夹角的大小为__________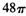 的球面上三点,且A
的球面上三点,且A B=2,BC=4,
B=2,BC=4,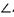 ABC=
ABC=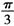 为球心,则二面角0-AB-C的大小为( )
为球心,则二面角0-AB-C的大小为( )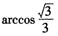 B.
B.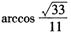 C.
C.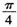 D.
D.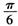
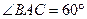 ,D为BC的中点。
,D为BC的中点。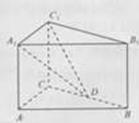
 1—C的大小。
1—C的大小。