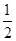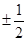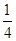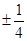题目内容
(本题满分12分)
设函数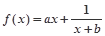 (
(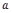 ,
,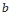 为常数),且方程
为常数),且方程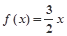 有两个实根为
有两个实根为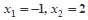 .
.
(1)求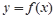 的解析式;
的解析式;
(2)证明:曲线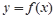 的图像是一个中心对称图形,并求其对称中心.
的图像是一个中心对称图形,并求其对称中心.
设函数
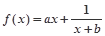 (
(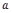 ,
,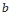 为常数),且方程
为常数),且方程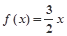 有两个实根为
有两个实根为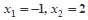 .
.(1)求
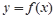 的解析式;
的解析式;(2)证明:曲线
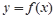 的图像是一个中心对称图形,并求其对称中心.
的图像是一个中心对称图形,并求其对称中心.(Ⅰ)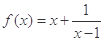 .(II)证明:见解析。
.(II)证明:见解析。
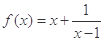 .(II)证明:见解析。
.(II)证明:见解析。本题考查用待定系数法求函数解析式,函数图象的平移.
(1) 把方程的2个实数根分别代入方程得到方程组,解此方程组求出待定系数,进而得到函数的解析式.
(2)利用2个奇函数的和仍是奇函数,再利用图象平移找出所求函数的对称中心。
解:(Ⅰ)由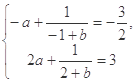 解得
解得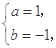
故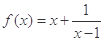 .
.
(II)证明:已知函数 ,
,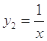 都是奇函数.
都是奇函数.
所以函数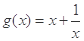 也是奇函数,其图像是以原点为中心的中心对称图形.
也是奇函数,其图像是以原点为中心的中心对称图形.
而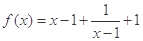 .
.
可知,函数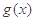 的图像沿
的图像沿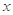 轴方向向右平移1个单位,再沿
轴方向向右平移1个单位,再沿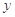 轴方向向上平移1个单位,即得到函数
轴方向向上平移1个单位,即得到函数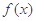 的图像,故函数
的图像,故函数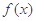 的图像是以点
的图像是以点 为中心的中心对称图形.
为中心的中心对称图形.
(1) 把方程的2个实数根分别代入方程得到方程组,解此方程组求出待定系数,进而得到函数的解析式.
(2)利用2个奇函数的和仍是奇函数,再利用图象平移找出所求函数的对称中心。
解:(Ⅰ)由
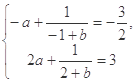 解得
解得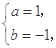
故
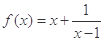 .
.(II)证明:已知函数
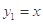 ,
,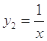 都是奇函数.
都是奇函数.所以函数
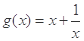 也是奇函数,其图像是以原点为中心的中心对称图形.
也是奇函数,其图像是以原点为中心的中心对称图形.而
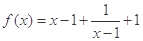 .
. 可知,函数
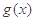 的图像沿
的图像沿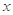 轴方向向右平移1个单位,再沿
轴方向向右平移1个单位,再沿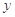 轴方向向上平移1个单位,即得到函数
轴方向向上平移1个单位,即得到函数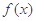 的图像,故函数
的图像,故函数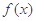 的图像是以点
的图像是以点 为中心的中心对称图形.
为中心的中心对称图形.
练习册系列答案
相关题目
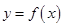 的局部图象,那么
的局部图象,那么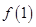 与
与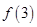 的大小关系正确的是 ( )
的大小关系正确的是 ( ) 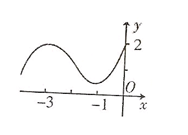
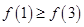
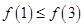
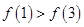

 +bx(a≠0),满足f(-4)=2,则f(4)的值为( )
+bx(a≠0),满足f(-4)=2,则f(4)的值为( ) 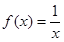 ,
,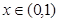 是
是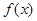 为
为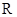 上的奇函数,当
上的奇函数,当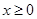 时,
时,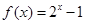 ,则当
,则当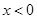 时,
时,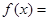 ___________.
___________.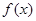 是定义在
是定义在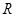 上的偶函数,并且
上的偶函数,并且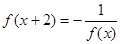 ,当
,当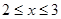 时,
时,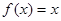 ,则
,则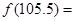 _________________.
_________________.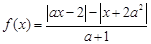 为奇函数,则实数a = .
为奇函数,则实数a = .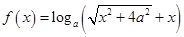 是奇函数,则
是奇函数,则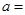 ( )
( )