题目内容
已知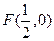 为抛物线
为抛物线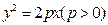 的焦点,点
的焦点,点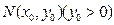 为其上一点,点M与点N关于x轴对称,直线
为其上一点,点M与点N关于x轴对称,直线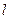 与抛物线交于异于M,N的A,B两点,且
与抛物线交于异于M,N的A,B两点,且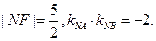
(I)求抛物线方程和N点坐标;
(II)判断直线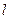 中,是否存在使得
中,是否存在使得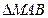 面积最小的直线
面积最小的直线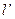 ,若存在,求出直线
,若存在,求出直线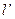 的方程和
的方程和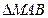 面积的最小值;若不存在,说明理由。
面积的最小值;若不存在,说明理由。
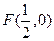 为抛物线
为抛物线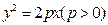 的焦点,点
的焦点,点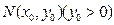 为其上一点,点M与点N关于x轴对称,直线
为其上一点,点M与点N关于x轴对称,直线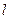 与抛物线交于异于M,N的A,B两点,且
与抛物线交于异于M,N的A,B两点,且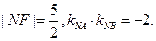
(I)求抛物线方程和N点坐标;
(II)判断直线
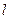 中,是否存在使得
中,是否存在使得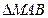 面积最小的直线
面积最小的直线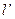 ,若存在,求出直线
,若存在,求出直线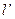 的方程和
的方程和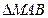 面积的最小值;若不存在,说明理由。
面积的最小值;若不存在,说明理由。(Ⅰ)有题意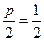 ,
, 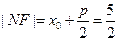 即
即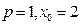 ,
,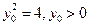 得
得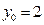
所以抛物线方程为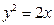 ,
,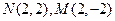 ………………………………4分
………………………………4分
(Ⅱ)由题意知直线的斜率不为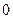 ,设直线
,设直线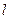 的方程为
的方程为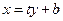 (
( )
)
联立方程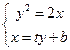 得
得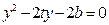 ,
,
设两个交点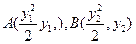
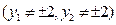
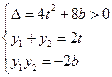 …………………………6分
…………………………6分
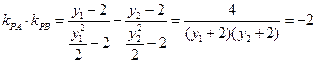 ,整理得
,整理得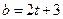 …………8分
…………8分
此时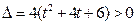 恒成立,
恒成立,
由此直线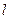 的方程可化为
的方程可化为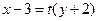 从而直线
从而直线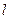 过定点
过定点 ……………9分
……………9分
因为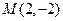 ,所以
,所以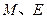 所在直线平行
所在直线平行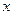 轴
轴
三角形 面积
面积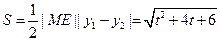 …………………………11分
…………………………11分
所以当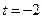 时
时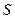 有最小值为
有最小值为 ,此时直线
,此时直线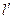 的方程为
的方程为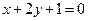 ……12分
……12分
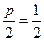 ,
, 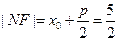 即
即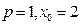 ,
,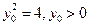 得
得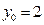
所以抛物线方程为
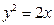 ,
,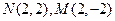 ………………………………4分
………………………………4分(Ⅱ)由题意知直线的斜率不为
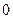 ,设直线
,设直线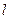 的方程为
的方程为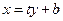 (
( )
)联立方程
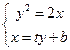 得
得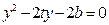 ,
,设两个交点
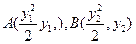
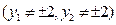
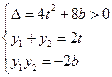 …………………………6分
…………………………6分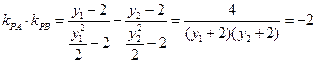 ,整理得
,整理得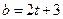 …………8分
…………8分此时
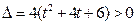 恒成立,
恒成立,由此直线
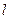 的方程可化为
的方程可化为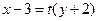 从而直线
从而直线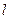 过定点
过定点 ……………9分
……………9分因为
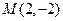 ,所以
,所以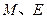 所在直线平行
所在直线平行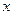 轴
轴三角形
 面积
面积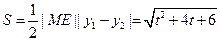 …………………………11分
…………………………11分所以当
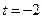 时
时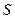 有最小值为
有最小值为 ,此时直线
,此时直线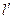 的方程为
的方程为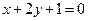 ……12分
……12分略

练习册系列答案
相关题目
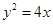 的焦点为F,过点M(-1,0)的直线在第一象限交抛物线于A、B,使
的焦点为F,过点M(-1,0)的直线在第一象限交抛物线于A、B,使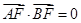 ,则直线AB的斜率
,则直线AB的斜率 ( )
( )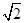 B
B  C
C 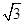 D
D 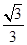
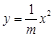 的焦点坐标为( ) .
的焦点坐标为( ) . 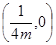
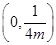
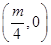
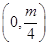
 m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?
m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?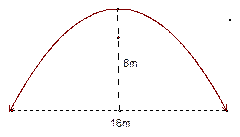
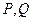 是抛物线
是抛物线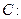
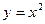 上两动点,直线
上两动点,直线 分别是抛物线
分别是抛物线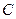 在点
在点 ,
,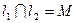 .
. 1)求点
1)求点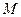 的纵坐标;
的纵坐标;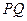 是否经过一定点
是否经过一定点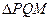 的面积的最小值
的面积的最小值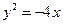 的准线方程是
的准线方程是 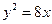 的焦点到准线的距离是( )高( )^ ((
的焦点到准线的距离是( )高( )^ ((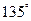 的直线,被抛物线所截得的弦长为8,试求抛物线的标准方程.
的直线,被抛物线所截得的弦长为8,试求抛物线的标准方程.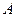 、
、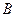 是抛物线
是抛物线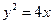 上的两个点,
上的两个点,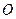 是坐标原点,若
是坐标原点,若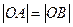 ,且
,且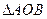 的垂心恰是抛物线的焦点,则
的垂心恰是抛物线的焦点,则