题目内容
19.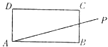 如图,在矩形ABCD中,AB=3,BC=$\sqrt{3}$,过点A向BAD所在区域等可能任作一条射线AP,则事件“射线AP与线段BC有公共点”发生的概率为( )
如图,在矩形ABCD中,AB=3,BC=$\sqrt{3}$,过点A向BAD所在区域等可能任作一条射线AP,则事件“射线AP与线段BC有公共点”发生的概率为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
分析 根据条件求出射线AP与线段BC有公共点时,对应角∠BAP的取值范围,利用几何概型的概率公式进行求解即可.
解答 解:∵“射线AP与线段BC有公共点”,
∴当P在C处满足条件,
∵AB=3,BC=$\sqrt{3}$,
∴tan∠BAP=$\frac{BC}{AB}=\frac{\sqrt{3}}{3}$,
即∠BAC=30°,
即当0°≤∠BAP≤30°时,射线AP与线段BC有公共点,
则对应的概率P=$\frac{30°-0°}{90°-0°}=\frac{1}{3}$,
故选:B.
点评 本题主要考查几何概型的应用,根据条件建立角度之间的关系是解决本题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
3.若某人每次射击击中目标的概率均为$\frac{3}{5}$,此人连续射击三次,至少有两次击中目标的概率为( )
| A. | $\frac{81}{125}$ | B. | $\frac{54}{125}$ | C. | $\frac{36}{125}$ | D. | $\frac{27}{125}$ |
4.棱长为2的正四面体ABCD在空间直角坐标系中移动,但保持点A、B分别在x轴、y轴上移动,则棱CD的中点E到坐标原点O的最远距离为( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$+1 | D. | $\sqrt{2}$+1 |
9.已知α为第二象限角,且sin(α+π)=-$\frac{4}{5}$,则tan2α=( )
| A. | $\frac{24}{7}$ | B. | $\frac{4}{5}$ | C. | -$\frac{24}{7}$ | D. | -$\frac{8}{3}$ |
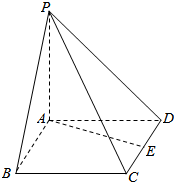 如图所示,四棱锥P-ABCD中,底面ABCD为菱形,且直线PA⊥平面ABCD,又棱PA=AB=2,E为CD的中点,∠ABC=60°.
如图所示,四棱锥P-ABCD中,底面ABCD为菱形,且直线PA⊥平面ABCD,又棱PA=AB=2,E为CD的中点,∠ABC=60°.