题目内容
3．若某人每次射击击中目标的概率均为$\frac{3}{5}$，此人连续射击三次，至少有两次击中目标的概率为（ ）| A． | $\frac{81}{125}$ | B． | $\frac{54}{125}$ | C． | $\frac{36}{125}$ | D． | $\frac{27}{125}$ |
分析 由条件利用n次独立重复实验中恰好发生k次的概率计算公式，求得恰有2次击中目标的概率、恰有3次击中目标的概率，再把这两个概率相加，即得所求．
解答 解：恰有2次击中目标的概率为${C}_{3}^{2}$•${（\frac{3}{5}）}^{2}$×$\frac{2}{5}$=$\frac{54}{125}$，恰有3次击中目标的概率为 ${（\frac{3}{5}）}^{3}$=$\frac{27}{125}$，
故至少有两次击中目标的概率为 $\frac{54}{125}$+$\frac{27}{125}$=$\frac{81}{125}$，
故选：A．
点评 本题主要考查n次独立重复实验中恰好发生k次的概率，等可能事件的概率，属于基础题．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
11．已知命题p：“?x∈[-5，0]，a≥ex”，命题q：“?x∈R，x2+4x+a=0”，若“p∧q”是真命题，则实数a的取值范围是（ ）
| A． | [e，4] | B． | [1，4] | C． | （4，+∞） | D． | （-∞，1] |
18．函数f（x）的定义域为R，f（-1）=3，对任意x∈R，f′（x）＜3，则f（x）＞3x+6的解集为（ ）
| A． | （-1，1） | B． | （-1，+∞） | C． | （-∞，-1） | D． | （-∞，+∞） |
8．天气预报报导在今后的三天中，每一天下雨的概率均为60%，这三天中恰有两天下雨的概率是（ ）
| A． | 0.432 | B． | 0.6 | C． | 0.8 | D． | 0.288 |
19．
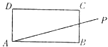如图，在矩形ABCD中，AB=3，BC=$\sqrt{3}$，过点A向BAD所在区域等可能任作一条射线AP，则事件“射线AP与线段BC有公共点”发生的概率为（ ）
如图，在矩形ABCD中，AB=3，BC=$\sqrt{3}$，过点A向BAD所在区域等可能任作一条射线AP，则事件“射线AP与线段BC有公共点”发生的概率为（ ）| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{1}{2}$ |