题目内容
7. 如图所示,四棱锥P-ABCD中,底面ABCD为菱形,且直线PA⊥平面ABCD,又棱PA=AB=2,E为CD的中点,∠ABC=60°.
如图所示,四棱锥P-ABCD中,底面ABCD为菱形,且直线PA⊥平面ABCD,又棱PA=AB=2,E为CD的中点,∠ABC=60°.(Ⅰ) 求证:直线EA⊥平面PAB;
(Ⅱ) 求直线AE与平面PCD所成角的正切值.
分析 (1)只需证明直线EA⊥AB,且EA⊥PA即可;
(2)先证明AH⊥平面PCD,得出∠AEP为直线AE与平面PCD所成角,在Rt△PAE中计算tan∠AEP的值.
解答 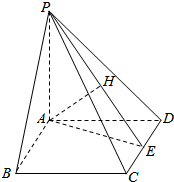 解:(1)证明:∵∠ADE=∠ABC=60°,ED=1,AD=2,
解:(1)证明:∵∠ADE=∠ABC=60°,ED=1,AD=2,
∴△AED是以∠AED为直角的Rt△;
又∵AB∥CD,∴EA⊥AB;
又PA⊥平面ABCD,∴EA⊥PA;
且AB∩PA=A,
∴EA⊥平面PAB;---------(7分)
(2)如图所示,连结PE,过A点作AH⊥PE于H点,
∵CD⊥EA,CD⊥PA,且PA∩EA=A,
∴CD⊥平面PAE;
又AH?平面PAE,
∴AH⊥CD;
又AH⊥PE,且CD∩AE=E,
∴AH⊥平面PCD,
∴∠AEP为直线AE与平面PCD所成角;------(11分)
在Rt△PAE中,∵PA=2,AE=$\sqrt{{AD}^{2}{-DE}^{2}}$=$\sqrt{3}$,
∴tan∠AEP=$\frac{PA}{AE}$=$\frac{2}{\sqrt{3}}$=$\frac{2\sqrt{3}}{3}$.----------(15分)
点评 本题考查了空间中的垂直关系的应用问题,也考查了空间想象能力与逻辑思维能力,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知命题p:“?x∈[-5,0],a≥ex”,命题q:“?x∈R,x2+4x+a=0”,若“p∧q”是真命题,则实数a的取值范围是( )
| A. | [e,4] | B. | [1,4] | C. | (4,+∞) | D. | (-∞,1] |
19. 如图,在矩形ABCD中,AB=3,BC=$\sqrt{3}$,过点A向BAD所在区域等可能任作一条射线AP,则事件“射线AP与线段BC有公共点”发生的概率为( )
如图,在矩形ABCD中,AB=3,BC=$\sqrt{3}$,过点A向BAD所在区域等可能任作一条射线AP,则事件“射线AP与线段BC有公共点”发生的概率为( )
 如图,在矩形ABCD中,AB=3,BC=$\sqrt{3}$,过点A向BAD所在区域等可能任作一条射线AP,则事件“射线AP与线段BC有公共点”发生的概率为( )
如图,在矩形ABCD中,AB=3,BC=$\sqrt{3}$,过点A向BAD所在区域等可能任作一条射线AP,则事件“射线AP与线段BC有公共点”发生的概率为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |