Question

【题目】设F1,F2分别为椭圆C

(1)若椭圆C上的点

(2)设点K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程;

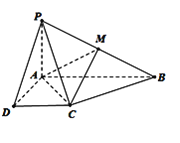
(3)已知椭圆具有性质:若M,N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM,PN的斜率都存在,并记为kPM,kPN时,那么kPM与kPN之积是与点P位置无关的定值,试写出双曲

Answer 1

【答案】（1）见解析；（2）；（3）见解析

【解析】

分析：（1）到两交点的距离之和为4，点在曲线上，列出的方程求解即可。

（2）设椭圆上的动点为，线段的中点,利用中点的坐标关系式，列出与的坐标关系，用表示出，代入椭圆方程即可。

（3）分别设出的坐标，表示出斜率化简整理即可。

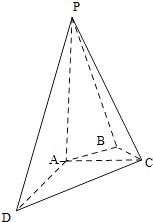
详解：(1)椭圆C的焦点在x轴上.由椭圆上的点A到F1,F2两点的距离之和是4,得2a=4,即a=2.

又点A,

∴+=1,b2=3.

∴c2=a2-b2=1.

∴椭圆C的方程+=1,焦点F1(-1,0),F2(1,0).

(2)设椭圆C上的动点为K(x1,y1),线段F1K的中点Q(x,y)满足:x=,y=,

∴x1=2x+1,y1=2y.

∴+=1,

+=1为所求的轨迹方程.

(3)类似的性质为:若M,N是双曲-=1(a>0,b>0)上关于原点对称的两个点,点P是双曲线上任意一点,当直线PM,PN的斜率都存在,并记为kPM,kPN时,那么kPM与kPN之积是与点P位置无关的定值.

证明:设点M的坐标为(m,n),则点N的坐标为(-m,-n),其-=1.

又设点P的坐标为(x,y),

∵kPM=,kPN=,

∴kPM·kPN=.

-=1,

∴x2=a2,m2=a2.

∴x2-m2=(y2-n2).

∴kPM·kPN=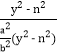=(定值).