题目内容
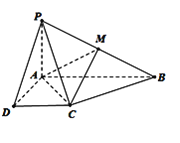
【题目】已知四棱锥P - ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC![]()
(1)证明平面PAD⊥平面PCD;
(2)求AC与PB所成角的余弦值;
(3)求平面AMC与平面BMC所成二面角的余弦值.
【答案】(1)见解析.
(2)![]() .
.
(3) -![]() .
.
【解析】分析:以A为坐标原点,AD长为单位长度,建立空间直角坐标系.
(1)求出![]() ,
,![]() ,计算
,计算![]() =0,推出AP⊥DC,然后证明DC⊥面PAD,即可证明面PAD⊥面PCD;
=0,推出AP⊥DC,然后证明DC⊥面PAD,即可证明面PAD⊥面PCD;
(2)利用空间向量的数量积,求AC与PB所成角的余弦值;
(3)![]() MC
MC![]() N(x,y,z),
N(x,y,z),![]() λ∈R,
λ∈R,![]() =λ
=λ![]() ,说明∠ANB为所求二面角的平面角,求出
,说明∠ANB为所求二面角的平面角,求出![]() ,计算
,计算![]() ,即可取得结果.
,即可取得结果.
详解: (1)因为PA⊥AD,PA⊥AB,AD⊥AB,所以可以以A为坐标原点,AD长为单位长度,建立空间直角坐标系.
如图,则各点坐标为A(0,0,0),B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),M![]() .
.

∵![]() =(0,0,1),
=(0,0,1),![]() =(0,1,0),
=(0,1,0),![]() =0,
=0,
∴AP⊥DC.
又由题设知:AD⊥DC,且AP与AD是平面PAD内的两条相交直线,由此得DC⊥面PAD.
又DC在面PCD内,故面PAD⊥面PCD.
![]() =(1,1,0),
=(1,1,0),![]() =(0,2,-1),
=(0,2,-1),
∴|![]() |=
|=![]() ,|
,|![]() |=
|=![]() ,
,![]() =2,
=2,
∴cos<![]() ,
,![]() >=
>=![]() =
=![]() .
.
![]() AC
AC![]() PB
PB![]() .
.
![]() MC
MC![]() N(x,y,z),
N(x,y,z),![]() λ∈R,
λ∈R,![]() =λ
=λ![]() ,
,
![]() =(1-x,1-y,-z),
=(1-x,1-y,-z),![]() =
=![]() ,
,
∴x=1-λ,y=1,z=![]() λ.
λ.
要使AN⊥MC,只![]() =0,即x-
=0,即x-![]() z=0,
z=0,
解得λ=![]() .可知当λ=
.可知当λ=![]() ,N点坐标
,N点坐标![]() ,
,
能![]() =0.
=0.
此时,![]() =
=![]() ,
,![]() =
=![]() ,
,
![]() =0.
=0.
![]() =0,
=0,![]() =0,得AN⊥MC,BN⊥MC.
=0,得AN⊥MC,BN⊥MC.
∴∠ANB为所求二面角的平面角.
∵|![]() |=
|=![]() ,|
,|![]() |=
|=![]() ,
,![]() =-
=-![]() ,
,
∴cos<![]() ,
,![]() >=
>=![]() =-
=-![]() .
.
故所求的二面角的余弦值为-![]() .
.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案【题目】某校举行汉字听写比赛,为了了解本次比赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题:
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 5 | 0.05 |
第2组 | [60,70) |
| 0.35 |
第3组 | [70,80) | 30 |
|
第4组 | [80,90) | 20 | 0.20 |
第5组 | [90,100] | 10 | 0.10 |
合计 | 100 | 1.00 |
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛,并从中选出2人做种子选手,求2人中至少有1人是第4组的概率。
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到数据如表所示(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | 8 | |
不肥胖 | 18 | ||
合计 | 30 |
(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有99%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
| 0.050 0.010 |
| 3.841 6.635 |
参考数据:
附:![]()