题目内容
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1. 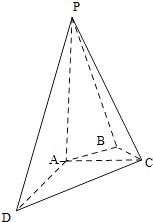
(1)证明:PC⊥AD;
(2)求二面角A﹣PC﹣D的正弦值;
(3)设E为棱PA上的点,满足异面直线BE与CD所成的角为30°,求AE的长.
【答案】
(1)[解法一] 如图,以A为原点,建立空间直角坐标系,则A(0,0,0),D(2,0,0),C(0,1,0),B(﹣ ![]() ,
, ![]() ,0),P(0,0,2).
,0),P(0,0,2).

证明:易得 ![]() =(0,1,﹣2),
=(0,1,﹣2), ![]() =(2,0,0),于是
=(2,0,0),于是 ![]()
![]() =0,所以PC⊥AD.
=0,所以PC⊥AD.
[解法二] 证明:由PA⊥平面ABCD,可得PA⊥AD,
又由AD⊥AC,PA∩AC=A,故AD⊥平面PAC,
又PC平面PAC,
所以PC⊥AD.
(2)[解法一] 解: ![]() =(0,1,﹣2),
=(0,1,﹣2), ![]() =(2,﹣1,0),设平面PCD的一个法向量为
=(2,﹣1,0),设平面PCD的一个法向量为 ![]() =(x,y,z),则
=(x,y,z),则  即
即 ![]()
取z=1,则以 ![]() =(1,2,1).又平面PAC的一个法向量为
=(1,2,1).又平面PAC的一个法向量为 ![]() =(1,0,0),于是cos<
=(1,0,0),于是cos< ![]() >=
>= ![]() =
= ![]() ,sin<
,sin< ![]() >=
>= ![]()
所以二面角A﹣PC﹣D的正弦值为 ![]()
[解法二] 解:如图,作AH⊥PC于点H,连接DH,
由PC⊥AD,PC⊥AH,可得PC⊥平面ADH,因此DH⊥PC,从而∠AHD为二面角A﹣PC﹣D的平面角.
在RT△PAC中,PA=2,AC=1,所以AH= ![]() ,由(1)知,AD⊥AH,在RT△DAH中,DH=
,由(1)知,AD⊥AH,在RT△DAH中,DH= ![]() =
= ![]() ,因此sin∠AHD=
,因此sin∠AHD= ![]() =
= ![]() .所以二面角A﹣PC﹣D的正弦值为
.所以二面角A﹣PC﹣D的正弦值为 ![]()

(3)解法一:设E(0,0,h),其中h∈[0,2],由此得 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,h).由
,h).由 ![]() =(2,﹣1,0),故cos<
=(2,﹣1,0),故cos< ![]() >=
>=  =
=  =
= ![]()
所以 ![]() =cos30°=
=cos30°= ![]() ,解得h=
,解得h= ![]() ,即AE=
,即AE= ![]() .
.
[解法二] 解:如图,因为∠ADC<45°,故过点B作CD的平行线必与线段AD相交,
设交点为F,连接BE,EF,故∠EBF(或其补角)为异面直线BE与CD所成的角.
由于BF∥CD,故∠AFB=∠ADC,在RT△DAC中,CD= ![]() ,sin∠ADC=
,sin∠ADC= ![]() ,故sin∠AFB=
,故sin∠AFB= ![]() .
.
在△AFB中,由 ![]() ,AB=
,AB= ![]() ,sin∠FAB=sin135°=
,sin∠FAB=sin135°= ![]() ,可得BF=
,可得BF= ![]() ,
,
由余弦定理,BF2=AB2+AF2﹣2ABAFcos∠FAB,得出AF= ![]() ,
,
设AE=h,在RT△EAF中,EF= ![]() =
= ![]() ,
,
在RT△BAE中,BE= ![]() =
= ![]() ,
,
在△EBF中,因为EF<BE,从而∠EBF=30°,
由余弦定理得到,cos30°= ![]() ,
,
解得h= ![]() ,
,
即AE= ![]() .
.

【解析】解法一(1)以A为原点,建立空间直角坐标系,通过得出 ![]()
![]() =0,证出PC⊥AD.(2)求出平面PCD,平面PCD的一个法向量,利用两法向量夹角求解.(3)设E(0,0,h),其中h∈[0,2],利用cos<
=0,证出PC⊥AD.(2)求出平面PCD,平面PCD的一个法向量,利用两法向量夹角求解.(3)设E(0,0,h),其中h∈[0,2],利用cos< ![]() >=cos30°=
>=cos30°= ![]() ,得出关于h的方程求解即可.解法二:(1)通过证明AD⊥平面PAC得出PC⊥AD.(2)作AH⊥PC于点H,连接DH,∠AHD为二面角A﹣PC﹣D的平面角.在RT△DAH中求解(3)因为∠ADC<45°,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF,故∠EBF(或其补角)为异面直线BE与CD所成的角.在△EBF中,因为EF<BE,从而∠EBF=30°,由余弦定理得出关于h的方程求解即可.
,得出关于h的方程求解即可.解法二:(1)通过证明AD⊥平面PAC得出PC⊥AD.(2)作AH⊥PC于点H,连接DH,∠AHD为二面角A﹣PC﹣D的平面角.在RT△DAH中求解(3)因为∠ADC<45°,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF,故∠EBF(或其补角)为异面直线BE与CD所成的角.在△EBF中,因为EF<BE,从而∠EBF=30°,由余弦定理得出关于h的方程求解即可.
【考点精析】解答此题的关键在于理解用空间向量求直线间的夹角、距离的相关知识,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.

 阅读快车系列答案
阅读快车系列答案【题目】某校准备从高一年级的两个男生![]() 和三个女生
和三个女生![]() 中选择2个人去参加一项比赛.
中选择2个人去参加一项比赛.
(1)若从这5个学生中任选2个人,求这2个人都是女生的概率;
(2)若从男生和女生中各选1个人,求这2个人包括![]() ,但不包括
,但不包括![]() 的概率.
的概率.
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到数据如表所示(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | 8 | |
不肥胖 | 18 | ||
合计 | 30 |
(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有99%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
| 0.050 0.010 |
| 3.841 6.635 |
参考数据:
附:![]()