题目内容
17.已知a∈$\left\{{x\left|{{{({\frac{1}{3}})}^x}-x=0}\right.}\right\}$,则$f(x)={log_a}^{({{x^2}-2x-3})}$的增区间为(-∞,-1).分析 根据函数$y=(\frac{1}{3})^{x}$和y=x的交点便可得出0<a<1,而可看出f(x)是由y=logat和t=x2-2x-3复合而成的复合函数,而函数y=logat为减函数,这样只要求函数t=x2-2x-3在f(x)定义域内的减区间便可得出f(x)的增区间.
解答 解:$y=(\frac{1}{3})^{x}$和y=x的交点横坐标x满足0<x<1;
即方程$(\frac{1}{3})^{x}-x=0$的解x满足0<x<1;
∴0<a<1;
令x2-2x-3=t,设y=f(x),则y=logat为减函数;
解x2-2x-3>0得,x<-1,或x>3;
∴函数t=x2-2x-3在(-∞,-1)∪(3,+∞)上的减区间便是函数f(x)的单调增区间;
∴f(x)的增区间为(-∞,-1).
故答案为:(-∞,-1).
点评 考查函数交点坐标和对应的方程解的关系,对数函数的单调性,以及复合函数的定义,复合函数单调区间的求法,二次函数单调区间的求法.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
7.已知函数f(x)=x2-x+2,则${∫}_{0}^{1}$f(x)dx=( )
| A. | $\frac{13}{6}$ | B. | $\frac{11}{6}$ | C. | 2 | D. | 3 |
8.已知$\frac{a+i}{b+2i}$=i(a,b∈R),其中i为虚数单位,则a+b=( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
12.下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的函数是( )
| A. | y=x3 | B. | $y=|{log_2^{\;}x}|$ | C. | y=2|x| | D. | y=-x2+1 |
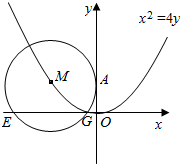 设圆M过点A(0,2),且圆心M在曲线C:x2=4y上,EG是圆M在x轴上截得的弦,试探究当M运动时.弦长|EG|是否为定值?为什么?
设圆M过点A(0,2),且圆心M在曲线C:x2=4y上,EG是圆M在x轴上截得的弦,试探究当M运动时.弦长|EG|是否为定值?为什么?