题目内容
【题目】定义行列式的运算如下：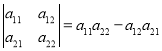
，已函数
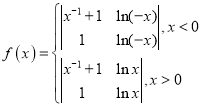以下命题正确的是（ ）
①对
，都有
；②若
，对
，总存在非零常数了，使得
；③若存在直线
与
的图象无公共点，且使的图案位于直线两侧，此直线即称为函数的分界线.则
的分界线的斜率的取值范围是
；④函数
的零点有无数个.
A.①③④B.①②④
C.②③D.①④
【答案】D
【解析】
根据行列式的运算定义可得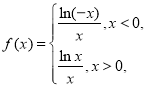
，根据奇函数定义可判断分段函数为奇函数，所以①正确；根据
的单调性和奇偶性可知不是周期函数，所以
不是周期函数，所以②错误；利用导数求出函数的过原点的切线的斜率，再根据的图像的对称性可得界线斜率的取值范围应为
，故③错误；根据在区间
上单调递减，
时，
，且
，可知
有无数个解，所以函数
的零点有无数个，④正确.
由题知,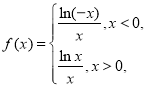
当
时,
,所以 
，同理
时亦有
，所以①正确；
又时，
，
，
，为奇函数，知的增区间为
，
，减区间为
，，则不存在周期性，故不是周期函数，所以②错误；
当时，过原点作的切线，设切点为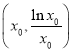
，则切线斜率
，由此直线过原点得
，所以
，结合②中在区间上单调递增；在区间上单调递减，且时，，且，可得时，的分界线的斜率的取值范围是，又为奇函数，可得时，的分界线的斜率的取值范围是.所以分界线斜率的取值范围应为，故③错误；
由上可知，在区间上单调递减，时，，且，所以有无数个解，所以函数的零点有无数个，④正确.
故选：D.
练习册系列答案
名校课堂系列答案
相关题目
