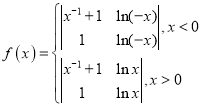题目内容
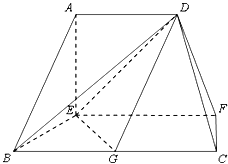
【题目】如图,四棱锥![]() 的侧棱
的侧棱![]() 与四棱锥
与四棱锥![]() 的侧棱
的侧棱![]() 都与底面
都与底面![]() 垂直,
垂直,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在点M,使平面
上是否存在点M,使平面![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?如果存在,指出M点的位置;如果不存在,请说明理由.
?如果存在,指出M点的位置;如果不存在,请说明理由.
【答案】(1)证明见解析;(2)存在,M点与F点重合
【解析】
(1)根据垂直于同一个平面的两条直线平行,可得![]() ,再根据勾股定理分别求出
,再根据勾股定理分别求出![]() ,即可证得四边形
,即可证得四边形![]() 为平行四边形,然后根据线面平行的判定定理即可证出;
为平行四边形,然后根据线面平行的判定定理即可证出;
(2)以点![]() 为原点,建立空间直角坐标系,设
为原点,建立空间直角坐标系,设![]() ,得到点
,得到点![]() 的坐标,再分别求出平面
的坐标,再分别求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,根据二面角的向量计算公式,即可建立方程,解出
的法向量,根据二面角的向量计算公式,即可建立方程,解出![]() ,即可确定M点的位置.
,即可确定M点的位置.
(1)∵![]() ,∴
,∴![]()
∵![]() ,
,![]() ,∴
,∴![]() ,同理可得
,同理可得![]()
又![]() ,
,![]() ,∴
,∴![]()
∵![]() ,∴四边形
,∴四边形![]() 为平行四边形,则
为平行四边形,则![]() ,而
,而![]() 平面
平面![]() ,
,![]() 平面
平面![]() ∴
∴![]() 平面
平面![]() .
.
(2)以D为原点建立如图所示的空间直角坐标系,如图所示: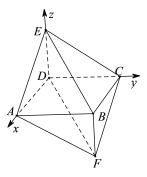
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
则![]() ,
,![]()
令![]() (
(![]() ),则
),则![]()
设平面![]() 的法向量
的法向量![]() ,则
,则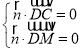
即![]() ,得
,得![]()
又平面![]() 的法向量
的法向量![]() ,
,
设平面![]() 与平面
与平面![]() 的夹角为
的夹角为![]() ,则
,则![]() ,
,![]()
∴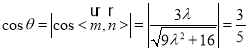 ,则
,则![]()
即:M点与F点重合时满足题意.

【题目】某班级有60名学生,学号分别为1~60,其中男生35人,女生25人.为了了解学生的体质情况,甲、乙两人对全班最近一次体育测试的成绩分别进行了随机抽样.其中一人用的是系统抽样,另一人用的是分层抽样,他们得到各12人的样本数据如下所示,并规定体育成绩大于或等于80人为优秀.
甲抽取的样本数据:
学号 | 4 | 9 | 14 | 19 | 24 | 29 | 34 | 39 | 44 | 49 | 54 | 59 |
性别 | 男 | 女 | 男 | 男 | 女 | 男 | 女 | 男 | 女 | 女 | 男 | 男 |
体育成绩 | 90 | 80 | 75 | 80 | 83 | 85 | 75 | 80 | 70 | 80 | 83 | 70 |
女抽取的样本数据:
学号 | 1 | 8 | 10 | 20 | 23 | 28 | 33 | 35 | 43 | 48 | 52 | 57 |
性别 | 男 | 男 | 男 | 男 | 男 | 男 | 男 | 女 | 女 | 女 | 女 | 女 |
体育成绩 | 95 | 85 | 85 | 80 | 70 | 80 | 80 | 65 | 70 | 60 | 70 | 80 |
(Ⅰ)在乙抽取的样本中任取4人,记这4人中体育成绩优秀的学生人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)请你根据乙抽取的样本数据,判断是否有95%的把握认为体育成绩是否为优秀和性别有关;
(Ⅲ)判断甲、乙各用的何种抽样方法,并根据(Ⅱ)的结论判断哪种抽样方法更优,说明理由.
附: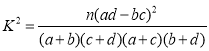
| 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |