题目内容
12.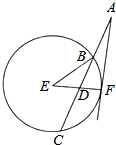 如图,过圆E外一点A作一条直线与圆E交B,C两点,且AB=$\frac{1}{3}$AC,作直线AF与圆E相切于点F,连接EF交BC于点D,己知圆E的半径为2,∠EBC=$\frac{π}{6}$.
如图,过圆E外一点A作一条直线与圆E交B,C两点,且AB=$\frac{1}{3}$AC,作直线AF与圆E相切于点F,连接EF交BC于点D,己知圆E的半径为2,∠EBC=$\frac{π}{6}$.(1)求AF的长;
(2)求证:AD=3ED.
分析 (1)延长BE交圆E于点M,连结CM,则可求BC=2$\sqrt{3}$,AB=$\frac{1}{2}BC=\sqrt{3}$,利用切割线定理即可求得AF的值.
(2)过E作EH⊥BC于H,可知△EDH与△ADF相似,由$\frac{ED}{AD}=\frac{EH}{AF}=\frac{1}{3}$,可求AD=3ED.
解答 解:(1)延长BE交圆E于点M,连结CM,则∠BCM=90°,
又BM=2BE=4,∠EBC=30°,所以BC=2$\sqrt{3}$,
又AB=$\frac{1}{3}AC$,可知AB=$\frac{1}{2}BC=\sqrt{3}$.
所以根据切割线定理AF2=AB•AC=$\sqrt{3}×3\sqrt{3}=9$,即AF=3.(5分)
(2)过E作EH⊥BC于H,则△EDH与△ADF相似,
从而有$\frac{ED}{AD}=\frac{EH}{AF}=\frac{1}{3}$,因此AD=3ED.(10分)
点评 本题主要考查了切割线定理的应用,考查了相似三角形的判定,与圆有关的比例线段,属于基本知识的考查.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
20.设直角三角形中两锐角为A和B,则cosAcosB的取值范围是( )
| A. | (0,$\frac{1}{2}$] | B. | (0,1) | C. | [$\frac{1}{2}$,1) | D. | [$\frac{\sqrt{3}}{4}$,1) |
2.若q<19,则将(x-q)(x-q-1)(x-q-2)•…•(x-19)写成A${\;}_{n}^{m}$的形式是( )
| A. | A${\;}_{x-q}^{x-19}$ | B. | A${\;}_{x-q}^{x-20}$ | C. | A${\;}_{x-q}^{19-q}$ | D. | A${\;}_{x-q}^{20-q}$ |