题目内容
2.若q<19,则将(x-q)(x-q-1)(x-q-2)•…•(x-19)写成A${\;}_{n}^{m}$的形式是( )| A. | A${\;}_{x-q}^{x-19}$ | B. | A${\;}_{x-q}^{x-20}$ | C. | A${\;}_{x-q}^{19-q}$ | D. | A${\;}_{x-q}^{20-q}$ |
分析 根据题意,利用排列数的计算公式,写出算式结果即可.
解答 解:(x-q)(x-q-1)(x-q-2)•…•(x-19)中,
共有[(x-q)-(x-19)+1]=(20-q)个连续自然数相乘,
且最大的自然数是(x-q),
∴写成A${\;}_{n}^{m}$的形式是${A}_{x-q}^{20-q}$.
故选:D.
点评 本题考查了排列数的计算公式问题,是基础题目.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
13.在密码学中,直接可以看到内容的为明码,对明码进行某种处理后得到的内容为密码.有一种密码将英文的26个字母a,b,c,…,z(不分大小写)依次对应1,2,3,…,26这26个自然数,见表:
给出明码对应的序号x和密码对应的序号y的变换公式:y=$\left\{\begin{array}{l}\frac{x+1}{2},x为奇数,且1≤x≤26\\ \frac{x}{2}+13,x为偶数,且1≤x≤26\end{array}$
利用它可以将明码转换成密码,如5→$\frac{5+1}{2}$=3,即e变成c,8→$\frac{8}{2}$+13=17,即h变成q.按上述公式,若将某明码译成的密码是shxc,那么原来的明码是love.
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
利用它可以将明码转换成密码,如5→$\frac{5+1}{2}$=3,即e变成c,8→$\frac{8}{2}$+13=17,即h变成q.按上述公式,若将某明码译成的密码是shxc,那么原来的明码是love.
12.函数f(x)=tan($\frac{1}{3}x$+$\frac{π}{6}$)的最小正周期为( )
| A. | 3π | B. | 6π | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
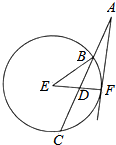 如图,过圆E外一点A作一条直线与圆E交B,C两点,且AB=$\frac{1}{3}$AC,作直线AF与圆E相切于点F,连接EF交BC于点D,己知圆E的半径为2,∠EBC=$\frac{π}{6}$.
如图,过圆E外一点A作一条直线与圆E交B,C两点,且AB=$\frac{1}{3}$AC,作直线AF与圆E相切于点F,连接EF交BC于点D,己知圆E的半径为2,∠EBC=$\frac{π}{6}$. 如图,在平面四边形ABCD中,AD=$\sqrt{6}$,CD=$\sqrt{2}$,∠ABD=60°,∠ADB=75°,
如图,在平面四边形ABCD中,AD=$\sqrt{6}$,CD=$\sqrt{2}$,∠ABD=60°,∠ADB=75°,