题目内容
(本小题满分12分)
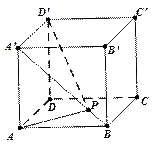
已知 矩形ABCD所在平面,PA=AD=
矩形ABCD所在平面,PA=AD= ,E为线段PD上一点。
,E为线段PD上一点。
(1)当E为PD的中点时,求证:
(2)是否存在E使二面角E—AC—D为30°?若存在,求 ,若不存在,说明理由。
,若不存在,说明理由。
已知
 矩形ABCD所在平面,PA=AD=
矩形ABCD所在平面,PA=AD= ,E为线段PD上一点。
,E为线段PD上一点。(1)当E为PD的中点时,求证:

(2)是否存在E使二面角E—AC—D为30°?若存在,求
 ,若不存在,说明理由。
,若不存在,说明理由。
①证明:不妨设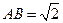 ,则
,则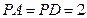 ,取AD的中点F,连EF,CF。易知
,取AD的中点F,连EF,CF。易知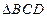 ∽
∽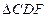 ,∴
,∴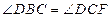
∴
∴BD⊥CF
又EF∥PA,PA⊥平面ABCD
∴EF⊥平面ABCD
故由三垂线定理知BD⊥CE(5分)
②作EG⊥AD于G,过G作GH⊥A C于H,连EH,则可证∠EHG为二面角E-AC-D的平面角。
C于H,连EH,则可证∠EHG为二面角E-AC-D的平面角。

设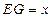 ,则
,则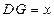 ,
,
∴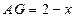 ,又
,又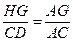 ,
,
∴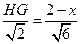 ,∴
,∴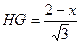 ,
,
∴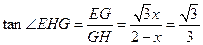 ,∴
,∴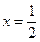 ,
,
所以存在点E满足条件,且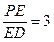 (7分)
(7分)
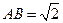 ,则
,则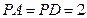 ,取AD的中点F,连EF,CF。易知
,取AD的中点F,连EF,CF。易知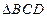 ∽
∽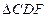 ,∴
,∴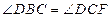
∴

∴BD⊥CF
又EF∥PA,PA⊥平面ABCD
∴EF⊥平面ABCD
故由三垂线定理知BD⊥CE(5分)
②作EG⊥AD于G,过G作GH⊥A
 C于H,连EH,则可证∠EHG为二面角E-AC-D的平面角。
C于H,连EH,则可证∠EHG为二面角E-AC-D的平面角。
设
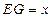 ,则
,则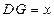 ,
,∴
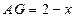 ,又
,又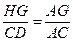 ,
,∴
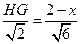 ,∴
,∴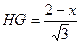 ,
,∴
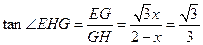 ,∴
,∴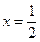 ,
,所以存在点E满足条件,且
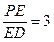 (7分)
(7分)略

练习册系列答案
相关题目
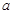 与平面
与平面 没有公共点,则
没有公共点,则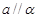 ;
; ,则
,则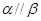
 是直角梯形,∠
是直角梯形,∠ =90°,
=90°, ∥
∥ ,
, =1,∠
=1,∠ =120°,
=120°, ⊥
⊥ ,直线
,直线 与直线
与直线 ⊥平面
⊥平面 ;
; 的体积;
的体积;
 和平面
和平面 ,给出下列三个命题:
,给出下列三个命题: 与
与 为异面直线,
为异面直线, ,则
,则 ∥
∥ ;
; ,
, ,则
,则 .
. 中,
中, 分别为BC, CC1中点,
分别为BC, CC1中点, 与
与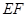 所成角的大小为
所成角的大小为








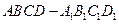 是棱长为2 cm的正方体.
是棱长为2 cm的正方体.
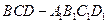 的体积;
的体积;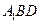 的距离;
的距离;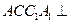 平面
平面 且法向量为
且法向量为 的平面的方程是
的平面的方程是 ”。现知道平面
”。现知道平面 的方程为
的方程为 ,则过
,则过 与
与 的直线与平面
的直线与平面 弦值是
弦值是 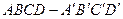 的面对角线
的面对角线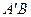 上存在一点
上存在一点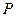 使得
使得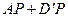 取得最小值,则此最小值为
取得最小值,则此最小值为