题目内容
(本题满分12分,(Ⅰ)小问4分,(Ⅱ)小问6分,(Ⅲ)小问2分.)
如图所示,直二面角 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
(Ⅰ)求证: ⊥平面
⊥平面
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求点 到平面
到平面 的距离.
的距离.

如图所示,直二面角
 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
(Ⅰ)求证:
 ⊥平面
⊥平面
(Ⅱ)求二面角
 的大小;
的大小;(Ⅲ)求点
 到平面
到平面 的距离.
的距离.
解:(Ⅰ)因为四边形 是边长为
是边长为 的正方形,所以
的正方形,所以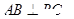 ,又二面角
,又二面角
 为直二面角,所以
为直二面角,所以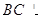 面
面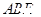 ,所以
,所以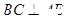 ①
①
又 ⊥平面
⊥平面 ,所以
,所以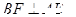 ②,
②,
由①②可得 ⊥平面
⊥平面 ………4分
………4分
(Ⅱ)由(Ⅰ)得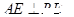 ,又
,又 ,所以
,所以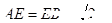 ,记
,记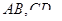 的中点分别为
的中点分别为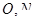 ,则以
,则以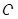 为坐标原点,以
为坐标原点,以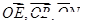 的方向为
的方向为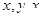 轴正方向建系
轴正方向建系
得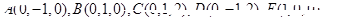 ………6分
………6分
则平面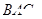 的法向量
的法向量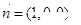 ,平面
,平面 的法向量
的法向量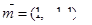 ………8分
………8分
所以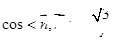 ,所以二面角
,所以二面角 的大小为
的大小为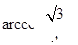 ………10分
………10分
(Ⅲ)因为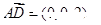 ,
,
所以点 到平面
到平面 的距离
的距离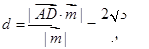 ………12分
………12分
 是边长为
是边长为 的正方形,所以
的正方形,所以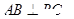 ,又二面角
,又二面角 为直二面角,所以
为直二面角,所以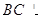 面
面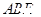 ,所以
,所以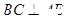 ①
①又
 ⊥平面
⊥平面 ,所以
,所以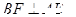 ②,
②,由①②可得
 ⊥平面
⊥平面 ………4分
………4分(Ⅱ)由(Ⅰ)得
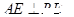 ,又
,又 ,所以
,所以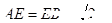 ,记
,记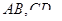 的中点分别为
的中点分别为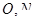 ,则以
,则以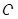 为坐标原点,以
为坐标原点,以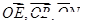 的方向为
的方向为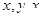 轴正方向建系
轴正方向建系得
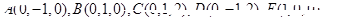 ………6分
………6分则平面
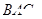 的法向量
的法向量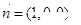 ,平面
,平面 的法向量
的法向量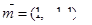 ………8分
………8分所以
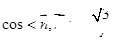 ,所以二面角
,所以二面角 的大小为
的大小为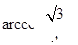 ………10分
………10分(Ⅲ)因为
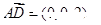 ,
,所以点
 到平面
到平面 的距离
的距离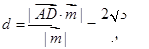 ………12分
………12分略

练习册系列答案
相关题目
 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。
 和平面
和平面 ,给出下列三个命题:
,给出下列三个命题: 与
与 为异面直线,
为异面直线, ,则
,则 ∥
∥ ;
; ,
, ,则
,则 .
. 中,
中, 为正方形
为正方形 中心,则
中心,则 与平面
与平面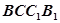 所成角的正切值为 ( )
所成角的正切值为 ( )



 中,
中, 分别为BC, CC1中点,
分别为BC, CC1中点, 与
与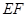 所成角的大小为
所成角的大小为








 内的一条直线平行,则m//
内的一条直线平行,则m//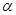
 ,则过
,则过
 ,则
,则
 为等边三角形,
为等边三角形, 为矩形,平面
为矩形,平面
 平面
平面 ,
, 分别为
分别为 、
、 、
、 中点,
中点, .
.
 的体积
的体积
 的侧面
的侧面 是菱形,
是菱形, 。
。 ;
; 上的点且
上的点且 ,求
,求 的值。
的值。
 中,三组对棱棱长分别相等且依次为
中,三组对棱棱长分别相等且依次为 、
、 、15,则此四面体
、15,则此四面体