题目内容
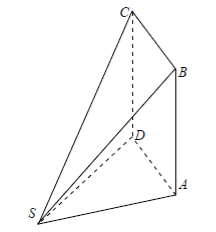
【题目】如图,多面体![]() 中,面
中,面![]() 为矩形,
为矩形,![]() ,且
,且![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)要证![]() 平面
平面![]() ,只需证明直线
,只需证明直线![]() 垂直平面
垂直平面![]() 内的两条相交直线
内的两条相交直线![]() 、
、![]() 即可;(2)要求
即可;(2)要求![]() 与
与![]() 所成的角,即求
所成的角,即求![]() 与
与![]() 所成的角,解三角形可求
所成的角,解三角形可求![]() 与
与![]() 所成角的余弦值;(3)过
所成角的余弦值;(3)过![]() 作
作![]() 于
于![]() 又过
又过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,说明
,说明![]() 为二面角
为二面角![]() 的平面角,解三角形可求二面角
的平面角,解三角形可求二面角![]() 的余弦值.
的余弦值.
试题解析:(1)∵![]() 是矩形,∴
是矩形,∴![]()
又![]() ,则
,则![]()
![]() , ∴
, ∴![]() 平面
平面![]()
(2)矩形![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴要求![]() 与
与![]() 所成的角,即求
所成的角,即求![]() 与
与![]() 所成的角.
所成的角.
在![]() 中,由(1)知
中,由(1)知![]() 面
面![]() ,
,
∴![]() 中,
中,![]() ,
,
∴![]() 是
是![]() 在面
在面![]() 内的射影,且
内的射影,且![]() ,
,
∴![]() ,
,
![]() ,
,
从而![]() 与
与![]() 的成的角的余弦为
的成的角的余弦为![]() ;
;
(3)∵![]() 中
中![]() ,且
,且![]() ,
,
∴![]() 面
面![]() ,
,
∴面![]() 面
面![]() ,
,![]() 为面
为面![]() 与面
与面![]() 的交线,
的交线,
∴过![]() 作
作![]() 于
于![]() ,∴
,∴![]() 面
面![]() ,
,
又过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,从而得:
,从而得:![]() ,
,
∴![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在矩形![]() 中,对角线
中,对角线![]() ,
,
∴在![]() 中,
中,![]() ,
,
由(2)知在![]() 中,
中,![]() ,
,
而![]() 中,
中,![]() ,且
,且![]() ,∴
,∴![]() ,
,
∴![]() 为等腰直角三角形且
为等腰直角三角形且![]() 为直角,
为直角,
∴![]() ,
,
∴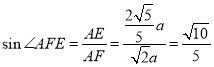 ,
,
所以所求的二面角的余弦为![]() .
.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
【题目】已知![]() 三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
| 6 |
| 7 | |
| 6 | 7 | 8 | |
| 5 | 6 | 7 | 8 |
(1)试估计![]() 班学生人数;
班学生人数;
(2)从![]() 班和
班和![]() 班抽出来的学生中各选一名,记
班抽出来的学生中各选一名,记![]() 班选出的学生为甲,
班选出的学生为甲,![]() 班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率.
班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率.