题目内容
【题目】已知二次函数f(x)满足f(x+1)-f(x)=-2x+1,且f(2)=15.
(1)求函数f(x)的解析式;
(2) 令g(x)=(2-2m)x-f(x).
① 若函数g(x)在x∈[0,2]上是单调函数,求实数m的取值范围;
② 求函数g(x)在x∈[0,2]上的最小值.
【答案】(1)f(x)=-x2+2x+15.(2)①m≤0或m≥2. ②见解析
【解析】试题分析:(1)设二次函数一般式f(x)=ax2+bx+c(a≠0),代入条件化简,根据恒等条件得2a=-2,a+b=1,解得a=-1,b=2.再根据f(2)=15,求c(2)①根据二次函数对称轴必在定义区间外得实数m的取值范围;②根据对称轴与定义区间位置关系,分三种情况讨论函数最小值取法.
试题解析:解:(1) 设二次函数f(x)=ax2+bx+c(a≠0),
则f(x+1)-f(x)=a(x+1)2+b(x+1)+c-(ax2+bx+c)=2ax+a+b=-2x+1,
∴ 2a=-2,a+b=1,∴ a=-1,b=2.
又f(2)=15,∴ c=15.
∴ f(x)=-x2+2x+15.
(2) ① ∵ f(x)=-x2+2x+15,
∴ g(x)=(2-2m)x-f(x)=x2-2mx-15.
又g(x)在x∈[0,2]上是单调函数,∴ 对称轴x=m在区间[0,2]的左侧或右侧,∴ m≤0或m≥2.
② g(x)=x2-2mx-15,x∈[0,2],对称轴x=m,
当m>2时,g(x)min=g(2)=4-4m-15=-4m-11;
当m<0时,g(x)min=g(0)=-15;
当0≤m≤2时,g(x)min=g(m)=m2-2m2-15=-m2-15.
综上所述,g(x)min=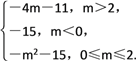

练习册系列答案
相关题目