题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,短轴两个端点为
,短轴两个端点为![]() ,且四边形
,且四边形![]() 是边长为2的正方形.
是边长为2的正方形.
(1)求椭圆的方程;
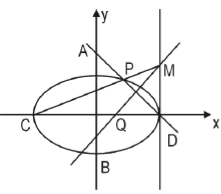
(2)若![]() 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点![]() 满足
满足![]() ,连结
,连结![]() ,交椭圆于点
,交椭圆于点![]() ,证明:
,证明:![]() 为定值;
为定值;
(3)在(2)的条件下,试问![]() 轴上是否存在异于点
轴上是否存在异于点![]() 的定点
的定点![]() ,使得以
,使得以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() 的交点,若存在,求出点
的交点,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)证明见解析;(3)存在,
;(2)证明见解析;(3)存在,![]() .
.
【解析】
试题分析:(1)由题意知![]() ,
,![]() ,
,![]() ,由此可知椭圆方程为
,由此可知椭圆方程为![]() ;(2)设
;(2)设![]() ,则直线
,则直线![]() :
:![]() ,代入椭圆方程
,代入椭圆方程![]() ,得
,得![]() ,然后利用根与系数的关系能够推导出
,然后利用根与系数的关系能够推导出![]() 为定值;(3)设存在
为定值;(3)设存在![]() 满足条件,则
满足条件,则![]() ,直线
,直线![]() 的斜率
的斜率![]() ,直线
,直线![]() 的斜率
的斜率![]() ,再由
,再由![]() ,由此可知存在
,由此可知存在![]() 满足条件.
满足条件.
试题解析:(1)![]() ,∴
,∴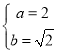 椭圆方程为:
椭圆方程为:![]() .
.
(2)∵![]() ,∴设
,∴设![]() ,则直线
,则直线![]() 的方程为:
的方程为:![]() ,
,
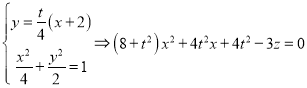 ,
,
解设:![]() 或
或![]() (舍去),
(舍去),
![]() ,∴
,∴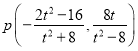 ,从而
,从而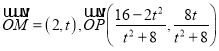 ,
,
∴![]() .
.
(3)设![]() ,若以
,若以![]() 为直径的圆过
为直径的圆过![]() 与
与![]() 的交点即直线
的交点即直线![]() ,
,
直线![]() 的斜率
的斜率![]() ,直线
,直线![]() 的斜率
的斜率![]() ,
,
所以![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() .
.

练习册系列答案
相关题目
【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区![]() 的年平均浓度不得超过
的年平均浓度不得超过![]() 微克/立方米,
微克/立方米,![]() 的24小时平均浓度不得超过
的24小时平均浓度不得超过![]() 微克/立方米.某城市环保部门随机抽取了一居民区去年20天
微克/立方米.某城市环保部门随机抽取了一居民区去年20天![]() 的24小时平均浓度的监测数据,数据统计如下:
的24小时平均浓度的监测数据,数据统计如下:
组别 |
(微克/立方米) | 频数(天) | 频率 |
第一组 |
| 3 | 0.15 |
第二组 |
| 12 | 0.6 |
第三组 |
| 3 | 0.15 |
第四组 |
| 2 | 0.1 |
(1)从样本中![]() 的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天
的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天
![]() 的24小时平均浓度超过75微克/立方米的概率;
的24小时平均浓度超过75微克/立方米的概率;
(2)求样本平均数,并根据样本估计总体的思想,从![]() 的年平均浓度考虑,判断该居民区的环境是
的年平均浓度考虑,判断该居民区的环境是
否需要改进?说明理由.