题目内容
已知f(x)＝x2－2(n＋1)x＋n2＋5n－7，
(1)设f(x)的图象的顶点的纵坐标构成数列{an}，求证：{an}为等差数列；
(2)设f(x)的图象的顶点到x轴的距离构成数列{bn}，求{bn}的前n项和Sn.
(1)设f(x)的图象的顶点的纵坐标构成数列{an}，求证：{an}为等差数列；
(2)设f(x)的图象的顶点到x轴的距离构成数列{bn}，求{bn}的前n项和Sn.
(1)证明：∵f(x)＝[x－(n＋1)]2＋3n－8，
∴an＝3n－8，
∵an＋1－an＝3，∴{an}为等差数列．
(2)∵bn＝|3n－8|，
当1≤n≤2时，bn＝8－3n，b1＝5.
Sn＝＝.
当n≥3时，bn＝3n－8，
Sn＝5＋2＋1＋4＋…＋(3n－8)
＝7＋＝.
∴Sn＝
∴an＝3n－8，
∵an＋1－an＝3，∴{an}为等差数列．
(2)∵bn＝|3n－8|，
当1≤n≤2时，bn＝8－3n，b1＝5.
Sn＝＝.
当n≥3时，bn＝3n－8，
Sn＝5＋2＋1＋4＋…＋(3n－8)
＝7＋＝.
∴Sn＝
略
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
的公比
， 
是
和
的一个等比中项，
和
的等差中项为
，若数列
满足
（
）．
的前
项和
．
为首项，
，则实数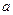
=" " ▲ ．
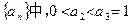，则使不等式（
）+（
）+（
）+……+（
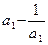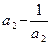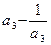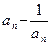）≤0成立的最大自然数n是____________。
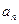}中，
，则 
＝_______.
中, 
求
的值
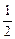a3、a1成等差数列，则
=" " ▲ 。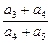