题目内容
【题目】如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2﹣4y﹣4=0,双曲线的左、右顶
点A、B是该圆与x轴的交点,双曲线与半圆相交于与x轴平行的直径的两端点.
(1)试求双曲线的标准方程;
(2)记双曲线的左、右焦点为F1、F2 , 试在“8”字形曲线上求点P,使得
∠F1PF2是直角.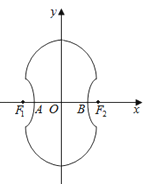
【答案】解:(1)上半个圆所在圆方程是x2+y2﹣4y﹣4=0,则圆心为(0,2),半径为2![]() .
.
则下半个圆所在圆的圆心为(0,﹣2),半径为2![]() .
.
双曲线的左、右顶点A、B是该圆与x轴的交点,即为(﹣2,0),(2,0),即a=2,
由于双曲线与半圆相交于与x轴平行的直径的两端点,则令y=2,解得,x=![]() 2
2![]() .
.
即有交点为(![]() 2
2![]() ,2).
,2).
设双曲线的方程为![]() =1(a>0,b>0),
=1(a>0,b>0),
则![]() =1,且a=2,解得,b=2.
=1,且a=2,解得,b=2.
则双曲线的方程为![]() =1;
=1;
(2)双曲线的左、右焦点为F1(﹣2![]() ,0),F2(2
,0),F2(2![]() ,0),
,0),
若∠F1PF2是直角,则设P(x,y),则有x2+y2=8,
由![]() 解得,x2=6,y2=2.
解得,x2=6,y2=2.
由![]() 解得,y=±1,不满足题意,舍去.
解得,y=±1,不满足题意,舍去.
故在“8”字形曲线上所求点P的坐标为(![]() ,
,![]() ),(﹣
),(﹣![]() ,
,![]() ),
),
(﹣![]() ,﹣
,﹣![]() ),(
),(![]() ,﹣
,﹣![]() ).
).
【解析】(1)求出半圆的圆心和半径,求得圆与x轴的交点,即有a=2,令y=2,解得交点,代入双曲线方程,解得b,进而得到双曲线的方程;
(2)求出焦点坐标,∠F1PF2是直角,则设P(x,y),则有x2+y2=8,联立两半圆的方程及双曲线方程,解得交点,注意检验,即可得到所求的P的坐标.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】已知函数f(x)=﹣x3+ax2﹣x﹣1在(﹣∞,+∞)上是单调函数,则实数a的取值范围是( )
A.[﹣![]() ,
, ![]() ]
]
B.(﹣![]() ,
, ![]() )
)
C.(﹣∞,﹣![]() )∪(
)∪(![]() , +∞)
, +∞)
D.(﹣∞,﹣![]() )∩(
)∩(![]() , +∞)
, +∞)
【题目】(本小题满分12分)某中学欲制定一项新的制度,学生会为此进行了问卷调查,所有参与问卷调查的人中,持有“支持”、“不支持”和“既不支持也不反对”的人数如下表所示:
支持 | 既不支持也不反对 | 不支持 | |
高一学生 | 800 | 450 | 200 |
高二学生 | 100 | 150 | 300 |
(Ⅰ)在所有参与问卷调查的人中,用分层抽样的方法抽取![]() 个人,已知从“支持”的人中抽取了45人,求
个人,已知从“支持”的人中抽取了45人,求![]() 的值;
的值;
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取5人,从这5人中任意选取2人,求至少有1人是高一学生的概率.