题目内容
如图,斜率为1的直线过抛物线 的焦点F,与抛物线交于两点A,B,
的焦点F,与抛物线交于两点A,B,
(1)若|AB|=8,求抛物线 的方程;
的方程;
(2)设C为抛物线弧AB上的动点(不包括A,B两点),求 的面积S的最大值;
的面积S的最大值;
(3)设P是抛物线 上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)
上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)
(1) (2)
(2) (3)
(3) ,设
,设
直线PA的方程
 ,
,


解析试题分析:设
(1)由条件知直线 由
由 消去y,得
消去y,得 ………1分
………1分
由题意,判别式 由韦达定理,
由韦达定理,
由抛物线的定义, 从而
从而 所求抛物的方程为
所求抛物的方程为 ………3分
………3分
(2)设 。由(1)易求得
。由(1)易求得
则 ,点C到直线
,点C到直线 的距离
的距离
将原点O(0,0)的坐标代入直线 的左边,得
的左边,得
而点C与原点O们于直线的同侧,由线性规划的知识知
因此 ……6分由(1),|AB|=4p。
……6分由(1),|AB|=4p。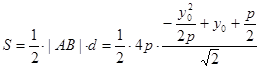

由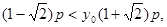 知当
知当 …8分
…8分
(3)由(2),易得 设
设 。
。
将 代入直线PA的方程
代入直线PA的方程
得 同理直线PB的方程为
同理直线PB的方程为
将 代入直线PA,PB的方程得
代入直线PA,PB的方程得




考点:直线与椭圆相交求弦长,三角型面积
点评:本题(1)中应用焦点弦公式 计算较简单,(2)(3)对于高二期末考试难度大,不建议采用
计算较简单,(2)(3)对于高二期末考试难度大,不建议采用

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 方程为
方程为 ,左、右焦点分别是
,左、右焦点分别是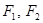 ,若椭圆
,若椭圆 到
到 .
.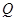 是椭圆
是椭圆 中点
中点 的轨迹方程;
的轨迹方程; 过定点
过定点 ,且与椭圆
,且与椭圆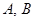 ,若
,若 为锐角(
为锐角( 为坐标原点),求直线
为坐标原点),求直线 的取值范围.
的取值范围. ),离心率为
),离心率为 .
.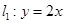 与直线
与直线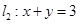 交于
交于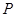 点.
点. 过
过 垂直时,求直线
垂直时,求直线 到直线
到直线 时,求直线
时,求直线 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线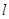 恰好与圆
恰好与圆 相切.
相切. 的离心率;
的离心率; 的最大值为49,求椭圆C
的最大值为49,求椭圆C ,并经过点
,并经过点 ,求此双曲线的标准方程.
,求此双曲线的标准方程.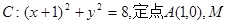 为圆上一动点,点
为圆上一动点,点 在
在 上,点
上,点 在
在 上,且满足
上,且满足 的轨迹为曲线
的轨迹为曲线 。
。
 求曲线
求曲线 若过定点F(0,2)的直线交曲线
若过定点F(0,2)的直线交曲线 (点
(点 在点
在点 之间),且满足
之间),且满足 ,求
,求 的取值范围。
的取值范围。 及直线
及直线 .
. 为何值时,直线与椭圆有公共点?
为何值时,直线与椭圆有公共点? ,求直线的方程.
,求直线的方程. 轴上,椭圆短轴的端点和焦点组成的四边形为正方形,且
轴上,椭圆短轴的端点和焦点组成的四边形为正方形,且 .
. 过点
过点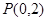 ,且与椭圆相交于
,且与椭圆相交于 、
、 不同的两点,当
不同的两点,当 面积取得最大值时,求直线
面积取得最大值时,求直线