题目内容
【题目】在直角坐标系xOy中,圆C的参数方程![]() (φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)直线l的极坐标方程是ρ(sinθ+![]() )=3
)=3![]() ,射线OM:θ=
,射线OM:θ=![]() 与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
【答案】(Ⅰ)![]() ;(Ⅱ)线段
;(Ⅱ)线段![]() 的长为2.
的长为2.
【解析】
试题分析:(Ⅰ)求圆![]() 的极坐标方程,首先得知道圆
的极坐标方程,首先得知道圆![]() 的普通方程,由圆
的普通方程,由圆![]() 的参数方程
的参数方程![]() 为参数),可得圆
为参数),可得圆![]() 的普通方程是
的普通方程是![]() ,由公式
,由公式![]() ,
,![]() ,
,![]() ,可得圆
,可得圆![]() 的极坐标方程,值得注意的是,参数方程化极坐标方程,必须转化为普通方程;(Ⅱ)求线段
的极坐标方程,值得注意的是,参数方程化极坐标方程,必须转化为普通方程;(Ⅱ)求线段![]() 的长,此问题处理方法有两种,一转化为普通方程,利用普通方程求出
的长,此问题处理方法有两种,一转化为普通方程,利用普通方程求出![]() 两点的坐标,有两点距离公式可求得线段
两点的坐标,有两点距离公式可求得线段![]() 的长,二利用极坐标方程求出
的长,二利用极坐标方程求出![]() 两点的极坐标,由于
两点的极坐标,由于![]() ,所以
,所以![]() ,所以线段
,所以线段![]() 的长为2.
的长为2.
试题解析:(Ⅰ)圆![]() 的普通方程是
的普通方程是![]() ,又
,又![]() ;所以圆
;所以圆![]() 的极坐标方程是
的极坐标方程是![]() .
.
(Ⅱ)设![]() 为点
为点![]() 的极坐标,则有
的极坐标,则有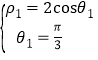 解得
解得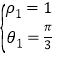 ,设
,设![]() 为点
为点![]() 的极坐标,则有
的极坐标,则有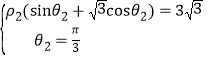 解得
解得 ,由于
,由于![]() ,所以
,所以![]() ,所以线段
,所以线段![]() 的长为2.
的长为2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目