题目内容
【题目】已知过点![]() 的椭圆
的椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() 、
、![]() ,
, ![]() 为椭圆上的任意一点,且
为椭圆上的任意一点,且![]() ,
, ![]() ,
, ![]() 成等差数列.
成等差数列.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() :
: ![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点,若点
两点,若点![]() 始终在以
始终在以![]() 为直径的圆外,求实数
为直径的圆外,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]() 或
或![]()
【解析】试题分析:(1)由题意,利用等差数列和椭圆的定义求出a、c的关系,再根据椭圆C过点A,求出a、b的值,即可写出椭圆C的标准方程;
(2)设P(x1,y1),Q(x2,y2),根据题意知x1=﹣2,y1=0;联立方程 消去y,由方程的根与系数关系求得x2、y2,由点A在以PQ为直径的圆外,得∠PAQ为锐角,
消去y,由方程的根与系数关系求得x2、y2,由点A在以PQ为直径的圆外,得∠PAQ为锐角, ![]()
![]() >0;由此列不等式求出k的取值范围.
>0;由此列不等式求出k的取值范围.
试题解析:
(1)∵![]() ,
, ![]() ,
, ![]() 成等差数列,
成等差数列,
∴![]() ,
,
由椭圆定义得![]() ,∴
,∴![]() ;
;
又椭圆![]() :
: ![]() (
(![]() )过点
)过点![]() ,
,
∴![]() ;∴
;∴![]() ,解得
,解得![]() ,
, ![]() ;
;
∴椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)设![]() ,
, ![]() ,联立方程
,联立方程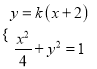 ,消去
,消去![]() 得:
得:
![]() ;
;
依题意![]() :
: ![]() 恒过点
恒过点![]() ,此点为椭圆的左顶点,∴
,此点为椭圆的左顶点,∴![]() ,
, ![]() ,①
,①
由方程的根与系数关系可得, ![]() ;②
;②
可得![]() ;③
;③
由①②③,解得![]() ,
, ![]() ;
;
由点![]() 在以
在以![]() 为直径的圆外,得
为直径的圆外,得![]() 为锐角,即
为锐角,即![]() ;
;
由![]() ,
, ![]() ,
,
∴![]() ;即
;即![]() ,
,
整理得, ![]() ,解得:
,解得: ![]() 或
或![]() .
.
∴实数![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.

【题目】已知函数y=a+bx与![]() ,若对于任意一点
,若对于任意一点![]() ,过点
,过点![]() 作与X轴垂直的直线,交函数y=a+bx的图象于点
作与X轴垂直的直线,交函数y=a+bx的图象于点![]() ,交函数
,交函数![]() 的图象于点
的图象于点![]() ,定义:
,定义:![]() ,若
,若![]() 则用函数y=a+bx来拟合Y与X之间的关系更合适,否则用函数
则用函数y=a+bx来拟合Y与X之间的关系更合适,否则用函数![]() 来拟合Y与X之间的关系
来拟合Y与X之间的关系
(1)给定一组变量P1(1,4),P2(2,5),p3(3,6),p4(4,5.5),p5(5,5.6),p6(6,5.8),对于函数![]() 与函数
与函数![]() ,试利用定义求Q1,Q2的值,并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;
,试利用定义求Q1,Q2的值,并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;
(2)若一组变量的散点图符合![]() 图象,试利用下表中的有关数据与公式求y对x的回归方程, 并预测当
图象,试利用下表中的有关数据与公式求y对x的回归方程, 并预测当![]() 时,
时,![]() 的值为多少.
的值为多少.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中的![]()
(附:对于一组数据![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为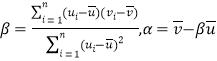 )
)


