题目内容
【题目】对于函数![]() ,若关系式
,若关系式![]() 中变量
中变量![]() 是变量
是变量![]() 的函数,则称函数
的函数,则称函数![]() 为可变换函数.例如:对于函数
为可变换函数.例如:对于函数![]() ,若
,若![]() ,则
,则![]() ,所以变量
,所以变量![]() 是变量
是变量![]() 的函数,所以
的函数,所以![]() 是可变换函数.
是可变换函数.
(1)求证:反比例函数![]() 不是可变换函数;
不是可变换函数;
(2)试判断函数![]() 是否是可变换函数并说明理由;
是否是可变换函数并说明理由;
(3)若函数![]() 为可变换函数,求实数
为可变换函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】分析:(1)利用反证法,假设![]() 是可变换函数,
是可变换函数,![]() ,利用关变量
,利用关变量![]() 的一元二次方程无解但导出矛盾,从而可得结论;(2)利用
的一元二次方程无解但导出矛盾,从而可得结论;(2)利用![]() 必须有交点,而
必须有交点,而![]() 连续且单调递减,值域为
连续且单调递减,值域为![]() ,
,![]() 连续且单调递增,值域为
连续且单调递增,值域为![]() ,进而可得结论;. (3)
,进而可得结论;. (3)![]() ,则
,则![]() 恒大于
恒大于![]() ,即无交点,不满足题意;若
,即无交点,不满足题意;若![]() ,则
,则![]() 必定有交点,即方程
必定有交点,即方程![]() 有解,从而可得结果.
有解,从而可得结果.
详解:(1)假设![]() 是可变换函数,则
是可变换函数,则![]() ,
,
因为变量![]() 是任意的,故当
是任意的,故当![]() 时,此时有关变量
时,此时有关变量![]() 的一元二次方程无解,
的一元二次方程无解,
则与假设矛盾,故原结论正确,得证;
(2)若![]() 是可变换函数,则
是可变换函数,则![]() ,
,
则有关![]() 的两个函数:
的两个函数:![]() 必须有交点,而
必须有交点,而![]() 连续且单调递减,值域为
连续且单调递减,值域为![]() ,
,
![]() 连续且单调递增,值域为
连续且单调递增,值域为![]() ,所以这两个函数
,所以这两个函数![]() 与
与![]() 必定有交点,
必定有交点,
即:变量![]() 是变量
是变量![]() 的函数,所以
的函数,所以![]() 是可变换函数;
是可变换函数;
(3)函数![]() 为可变换函数,则
为可变换函数,则![]() ,
,
若![]() ,则
,则![]() 恒大于
恒大于![]() ,即无交点,不满足题意;
,即无交点,不满足题意;
若![]() ,则
,则![]() 必定有交点,即方程
必定有交点,即方程![]() 有解,从而满足题意.
有解,从而满足题意.

【题目】已知函数y=a+bx与![]() ,若对于任意一点
,若对于任意一点![]() ,过点
,过点![]() 作与X轴垂直的直线,交函数y=a+bx的图象于点
作与X轴垂直的直线,交函数y=a+bx的图象于点![]() ,交函数
,交函数![]() 的图象于点
的图象于点![]() ,定义:
,定义:![]() ,若
,若![]() 则用函数y=a+bx来拟合Y与X之间的关系更合适,否则用函数
则用函数y=a+bx来拟合Y与X之间的关系更合适,否则用函数![]() 来拟合Y与X之间的关系
来拟合Y与X之间的关系
(1)给定一组变量P1(1,4),P2(2,5),p3(3,6),p4(4,5.5),p5(5,5.6),p6(6,5.8),对于函数![]() 与函数
与函数![]() ,试利用定义求Q1,Q2的值,并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;
,试利用定义求Q1,Q2的值,并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;
(2)若一组变量的散点图符合![]() 图象,试利用下表中的有关数据与公式求y对x的回归方程, 并预测当
图象,试利用下表中的有关数据与公式求y对x的回归方程, 并预测当![]() 时,
时,![]() 的值为多少.
的值为多少.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中的![]()
(附:对于一组数据![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为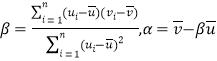 )
)

