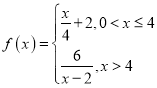题目内容
【题目】对于函数![]() ,若存在正实数
,若存在正实数![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 在
在![]() 上是有界函数,下列函数:
上是有界函数,下列函数:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
其中在![]() 上是有界函数的序号为________.
上是有界函数的序号为________.
【答案】②
【解析】
求出①②③④中各函数![]() 在
在![]() 上的值域,结合题中的定义进行判断即可.
上的值域,结合题中的定义进行判断即可.
对于①中的函数![]() ,当
,当![]() 时,
时,![]() ,该函数在
,该函数在![]() 上的值域为
上的值域为![]() ,所以,不存在正实数
,所以,不存在正实数![]() ,对于任意
,对于任意![]() ,使得
,使得![]() 成立;
成立;
对于②中的函数![]() ,当
,当![]() 时,
时,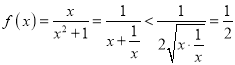 ,又
,又![]() ,
,![]() ,该函数在
,该函数在![]() 上的值域为
上的值域为![]() ,所以,存在正实数
,所以,存在正实数![]() ,当
,当![]() 时,对于任意
时,对于任意![]() ,都有
,都有![]() ;
;
对于③中的函数![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,该函数在
,该函数在![]() 上的值域为
上的值域为![]() ,所以,不存在正实数
,所以,不存在正实数![]() ,对于任意
,对于任意![]() ,使得
,使得![]() 成立;
成立;
对于④中的函数![]() ,取
,取![]() ,则
,则![]() ,
,
![]() ,同理,取
,同理,取![]() ,
,![]() ,
,![]() ,所以,函数
,所以,函数![]() 在
在![]() 上的值域为
上的值域为![]() ,所以,不存在正实数
,所以,不存在正实数![]() ,对于任意
,对于任意![]() ,使得
,使得![]() 成立.
成立.
综上所述:在![]() 上是有界函数的序号为②,故答案为:②.
上是有界函数的序号为②,故答案为:②.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目