题目内容
【题目】如图,己知抛物线![]() ,直线
,直线![]() 交抛物线于
交抛物线于![]() 两点,
两点,![]() 是抛物线外一点,连接
是抛物线外一点,连接![]() 分别交地物线于点
分别交地物线于点![]() ,且
,且![]() .
.

(1)若![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
(2)若![]() ,且
,且![]() 平行x轴,求
平行x轴,求![]() 面积.
面积.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)设![]() ,根据向量关系可用
,根据向量关系可用![]() 的坐标表示
的坐标表示![]() 的坐标,利用
的坐标,利用![]() 在抛物线可得
在抛物线可得![]() 的坐标满足的方程,同理利用D在抛物线也可得
的坐标满足的方程,同理利用D在抛物线也可得![]() 的坐标满足的方程,联立直线方程和抛物线方程结合韦达定理可得
的坐标满足的方程,联立直线方程和抛物线方程结合韦达定理可得![]() 的横坐标为2.也可以利用
的横坐标为2.也可以利用![]() 在抛物线上及
在抛物线上及![]() 得到
得到![]() ,利用
,利用![]() 、
、![]() 的中点、
的中点、![]() 的中点共线得到
的中点共线得到![]() 的横坐标为2.
的横坐标为2.
(2)根据(1)的相关结果可用![]() 表示
表示![]() 的坐标、
的坐标、![]() 的坐标及
的坐标及![]() 中点
中点![]() 的坐标,根据
的坐标,根据![]() 在抛物线上可得
在抛物线上可得![]() 的值并求出
的值并求出![]() 的坐标,最后利用公式
的坐标,最后利用公式![]() 可求面积.
可求面积.
(1)解法1:![]() ,设
,设![]() ,
,
则![]() ,由
,由![]() 可得
可得
![]() ,故
,故![]() ,同理
,同理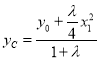 ,
,
故 ,代入抛物线得:
,代入抛物线得: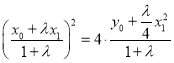 ,
,
化简得:![]() ,
,
同理得:![]() ,
,
所以![]() 为方程
为方程![]() 的两根,
的两根,
又由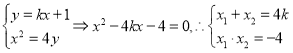 ,
,
将![]() 代入
代入![]() 且
且![]() ①,
①,
将![]() 代入①,得
代入①,得![]() ,故
,故![]() .
.
故点P的轨迹方程为![]() .
.
解法2:同解法1知![]()
![]() ,
,
设线段![]() 的中点分别为
的中点分别为![]() ,易知
,易知![]() 三点共线,
三点共线,
![]() (
(![]() 为实数),所以
为实数),所以![]() .
.
以下同解法1.
(2)由![]() 为方程
为方程![]() 的两根,
的两根,
可得:![]() .
.
由(1)得![]() ,因为
,因为![]() ,所以
,所以![]() ,故
,故![]() .
.
![]() 轴且
轴且![]() 在抛物线上,∴
在抛物线上,∴![]() 关于
关于![]() 轴对称.
轴对称.
![]() ,
,![]() 及
及![]() ,
,
 且
且![]() .
.
∵![]() 在抛物线上,
在抛物线上,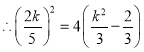 ,解得
,解得![]() .
.
设![]() 的中点为
的中点为![]() ,则
,则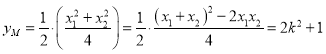 ,
,
所以![]() ,
,
而![]() .
.

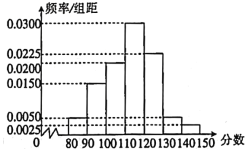
【题目】某市一次全市高中男生身高统计调查数据显示:全市10万名男生的身高服从正态分布![]() .现从某学校高中男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和190cm之间,将身高的测量结果按如下方式分成5组:第1组[160,166),第2组[166,172),...,第5组[184,190]下表是按上述分组方法得到的频率分布表:
.现从某学校高中男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和190cm之间,将身高的测量结果按如下方式分成5组:第1组[160,166),第2组[166,172),...,第5组[184,190]下表是按上述分组方法得到的频率分布表:
分组 | [160,166) | [166,172) | [172,178) | [178,184) | [184,190] |
人数 | 3 | 10 | 24 | 10 | 3 |
这50个数据的平均数和方差分别比10万个数据的平均数和方差多1和6.68,且这50个数据的方差为![]() .(同组中的身高数据用该组区间的中点值作代表):
.(同组中的身高数据用该组区间的中点值作代表):
(1)求![]() ,
,![]() ;
;
(2)给出正态分布的数据:![]() ,
,![]() .
.
(i)若从这10万名学生中随机抽取1名,求该学生身高在(169,179)的概率;
(ii)若从这10万名学生中随机抽取1万名,记![]() 为这1万名学生中身高在(169,184)的人数,求
为这1万名学生中身高在(169,184)的人数,求![]() 的数学期望.
的数学期望.
【题目】某地区实施“光盘行动”以后,某自助啤酒吧也制定了自己的行动计划,进店的每一位客人需预交![]() 元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足
元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足![]() 升的,按
升的,按![]() 升计算(如剩余
升计算(如剩余![]() 升,记为剩余
升,记为剩余![]() 升).例如:结账时,某桌剩余酒量恰好为
升).例如:结账时,某桌剩余酒量恰好为![]() 升,则该桌的每位客人还应付
升,则该桌的每位客人还应付![]() 元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的
元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的![]() 组数据
组数据![]() (其中
(其中![]() 表示饮酒人数,
表示饮酒人数,![]() (升)表示饮酒量):
(升)表示饮酒量):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
剩余酒量(单位:升) |
|
|
|
|
|
结账时的倍率 |
|
|
|
|
|
(1)求由这![]() 组数据得到的
组数据得到的![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)小王约了![]() 位朋友坐在一桌饮酒,小王及朋友用量杯共量取了
位朋友坐在一桌饮酒,小王及朋友用量杯共量取了![]() 升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请
升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请![]() 位或
位或![]() 位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
参考数据:回归直线的方程是![]() ,其中
,其中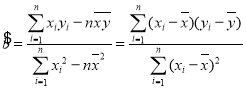 ,
,![]() .
.