题目内容
【题目】如图，在四棱锥P﹣ABCD中，AD∥BC，AB⊥AD，E是AB的中点，AB=AD=PA=PB=2，BC=1，PC= 
． 
（1）求证：CF∥平面PAB；
（2）求证：PE⊥平面ABCD；
（3）求二面角B﹣PA﹣C的余弦值．
【答案】
（1）证明：取AP的中点M，连接MF，MB，
因为M是AP中点，F是PD中点，
所以 
，
又因为 
，
所以四边形BCFM是平行四边形，所以FC∥BM，
又FC面ABP，BM面ABP
所以FC∥面ABP
（2）证明：连接CE，
因为在△ABP中，AB=AP=BP，点E是边AB在的中点，
所以PE⊥AB且 
，
在Rt△BEC中，BE=EC=1，EB⊥BC，所以 
在△PEC中， 
， ， 
，
所以PE⊥EC
又因为AB∩EC=E，AB面ABCD，EC面ABCD
所以PE⊥面ABCD
（3）解：取CD中点N，以EB，EN，EP分别为轴x，y轴，z轴，建立空间直角坐标系，各点坐标为：B（1，0，0），C（1，1，0），B（1，0，0）， 
，A（﹣1，0，0），
因为：BC⊥PE，AB⊥BC，所以BC⊥面ABP，面ABP的法向量为 
设面ABP的法向量为 
， 
，
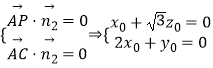，取x0=1，得 
，
由图可知二面角为锐二面角，设锐二面角为θ，
，
二面角B﹣PA﹣C余弦值为 
．
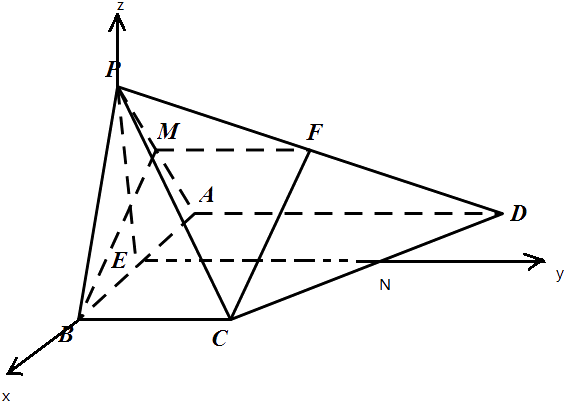
【解析】（1）取AP的中点M，连接MF，MB，推导出四边形BCFM是平行四边形，从而FC∥BM，由此能证明FC∥面ABP．（2）连接CE，推导出PE⊥AB，PE⊥EC，由此能证明PE⊥面ABCD．（3）取CD中点N，以EB，EN，EP分别为轴x，y轴，z轴，建立空间直角坐标系，利用向量法能求出二面角B﹣PA﹣C余弦值．
【考点精析】根据题目的已知条件，利用直线与平面平行的判定和直线与平面垂直的判定的相关知识可以得到问题的答案，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．
