题目内容
【题目】已知定点M（1，0）和直线x=﹣1上的动点N（﹣1，t），线段MN的垂直平分线交直线y=t于点R，设点R的轨迹为曲线E．
（1）求曲线E的方程；
（2）直线y=kx+b（k≠0）交x轴于点C，交曲线E于不同的两点A，B，点B关于x轴的对称点为点P．点C关于y轴的对称点为Q，求证：A，P，Q三点共线．
【答案】
（1）解：由题意可知：RN=RM，即点R到直线x=﹣1和点M的距离相等．
根据抛物线的定义可知：R的轨迹为抛物线，其中M为焦点．
设R的轨迹方程为：y2=2px， 
，p=2
所以R的轨迹方程为：y2=4x
（2）证明：由条件可知 
，则 
．
联立 
，消去y得k2x2+（2bk﹣4）x+b2=0，△=（2bk﹣4）2﹣4b2k2=16（1﹣bk）＞0．
设A（x1，y1），B（x2，y2）（x1＜x2），则P（x2，﹣y2）
， 
， 
．
因为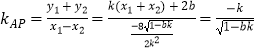 
， 
所以kAP=kAQ，
所以A，P，Q三点共线．
【解析】（1）由题意可知：RN=RM，即点R到直线x=﹣1和点M的距离相等，利用抛物线的定义求曲线E的方程；（2）联立 ，消去y，证明kAP=kAQ ， 可得A，P，Q三点共线．
练习册系列答案
天天练口算系列答案
相关题目
