题目内容
已知函数f(x)=(
+
)x2+bx+6(a,b为常数,a>1),且f(lglog81000)=8,则f(lglg2)的值是______.
| 1 |
| ax-1 |
| 1 |
| 2 |
∵函数f(x)=(
+
)x2+bx+6(a,b为常数,a>1),
∴f(x)-6=(
+
)x2+bx,
构造函数F(x)=f(x)-6=(
+
)x2+bx=
x2+bx=
x2+bx,
则F(-x)=
x2-bx=-[
x2+bx]=-F(x),
∴函数F(x)是奇函数.
∵lglog81000=lg(
)=lg(
)=lg(
)-lg(lg2),
∴f(lglog81000)=f(-lg(lg2))=8,
∵函数F(x)=f(x)-6是奇函数.
∴F(-lg(lg2))=-F(lg(lg2)),
即f(-lg(lg2))-6=-[f(lg(lg2))-6],
∴8-6=-f(lg(lg2))+6,
即f(lg(lg2))=4,
故答案为:4.
| 1 |
| ax-1 |
| 1 |
| 2 |
∴f(x)-6=(
| 1 |
| ax-1 |
| 1 |
| 2 |
构造函数F(x)=f(x)-6=(
| 1 |
| ax-1 |
| 1 |
| 2 |
| 2+ax-1 |
| 2(ax-1) |
| ax+1 |
| 2(ax-1) |
则F(-x)=
| 1+ax |
| 2(1-ax) |
| ax+1 |
| 2(ax-1) |
∴函数F(x)是奇函数.
∵lglog81000=lg(
| lg1000 |
| lg8 |
| 3 |
| 3lg2 |
| 1 |
| lg2 |
∴f(lglog81000)=f(-lg(lg2))=8,
∵函数F(x)=f(x)-6是奇函数.
∴F(-lg(lg2))=-F(lg(lg2)),
即f(-lg(lg2))-6=-[f(lg(lg2))-6],
∴8-6=-f(lg(lg2))+6,
即f(lg(lg2))=4,
故答案为:4.

练习册系列答案
相关题目
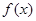 是定义在R上的奇函数,当
是定义在R上的奇函数,当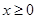 时
时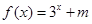 (m为常数),则
(m为常数),则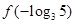 的值为( ).
的值为( ).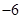
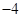
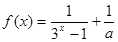 是奇函数,则
是奇函数,则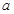 的值为( )
的值为( )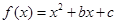 为偶函数,曲线
为偶函数,曲线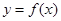 过点
过点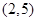 ,
, 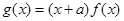 .
.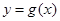 有斜率为0的切线,求实数
有斜率为0的切线,求实数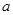 的取值范围;
的取值范围;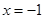 时函数
时函数