题目内容
已知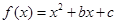 为偶函数,曲线
为偶函数,曲线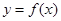 过点
过点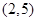 ,
, 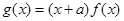 .
.
(1)若曲线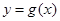 有斜率为0的切线,求实数
有斜率为0的切线,求实数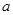 的取值范围;
的取值范围;
(2)若当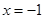 时函数
时函数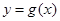 取得极值,确定
取得极值,确定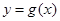 的单调区间.
的单调区间.
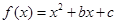 为偶函数,曲线
为偶函数,曲线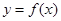 过点
过点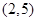 ,
, 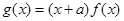 .
.(1)若曲线
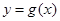 有斜率为0的切线,求实数
有斜率为0的切线,求实数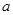 的取值范围;
的取值范围;(2)若当
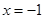 时函数
时函数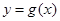 取得极值,确定
取得极值,确定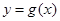 的单调区间.
的单调区间.(1) 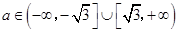 ;(2)
;(2)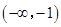 和
和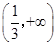 为
为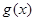 的单调递增区间,
的单调递增区间,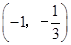 为
为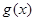 的单调递增区间.
的单调递增区间.
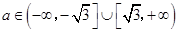 ;(2)
;(2)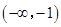 和
和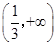 为
为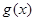 的单调递增区间,
的单调递增区间,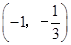 为
为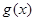 的单调递增区间.
的单调递增区间.试题分析:(1)先根据
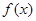 为偶函数,得到
为偶函数,得到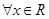 ,恒有
,恒有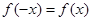 ,进而计算出
,进而计算出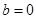 (也可根据二次函数的图像与性质得到对称轴
(也可根据二次函数的图像与性质得到对称轴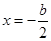 ,该对称轴为
,该对称轴为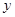 轴,进而得出
轴,进而得出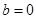 ),然后将点
),然后将点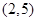 代入求出
代入求出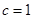 ,进而写出
,进而写出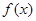 的表达式,此时
的表达式,此时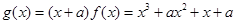 ,根据条件
,根据条件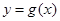 有斜率为0的切线即
有斜率为0的切线即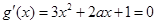 有实数解,根据二次方程有解的条件可得
有实数解,根据二次方程有解的条件可得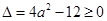 ,求解出
,求解出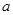 的取值范围即可;(2)先根据
的取值范围即可;(2)先根据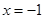 时函数
时函数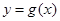 取得极值,得到
取得极值,得到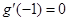 ,进而求出
,进而求出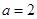 ,然后确定导函数
,然后确定导函数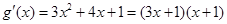 ,由导数
,由导数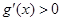 可求出函数的单调增区间,由
可求出函数的单调增区间,由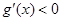 可求出函数的单调减区间.
可求出函数的单调减区间.(1)
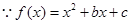 为偶函数,故对
为偶函数,故对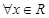 ,总有
,总有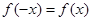 ,易得
,易得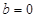
又曲线
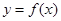 过点
过点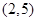 ,得
,得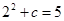 ,得
,得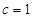 ,
,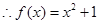 3分
3分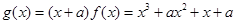
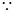 曲线
曲线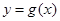 有斜率为0的切线,故
有斜率为0的切线,故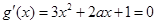 有实数解
有实数解此时有
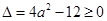 ,解得
,解得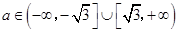 5分
5分(2)因
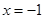 时函数
时函数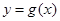 取得极值,故有
取得极值,故有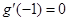 ,解得
,解得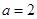
又
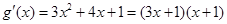 ,令
,令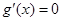 ,得
,得 .
.当
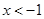 时,
时,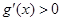
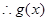 在
在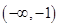 上为增函数
上为增函数当
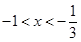 时,
时,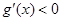 ,
,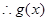 在
在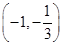 上为减函数
上为减函数当
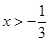 时,
时,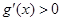 ,
,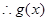 在
在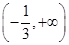 上为增函数
上为增函数从而
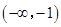 和
和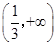 为
为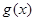 的单调递增区间,
的单调递增区间,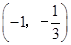 为
为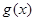 的单调递增区间 10分.
的单调递增区间 10分.
练习册系列答案
相关题目
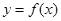 的图象由两条射线和三条线段组成.若
的图象由两条射线和三条线段组成.若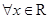 ,
,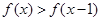 ,则正实数
,则正实数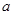 的取值范围是 .
的取值范围是 .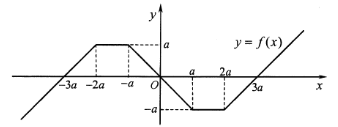
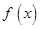 的定义域为D,如果
的定义域为D,如果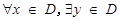 ,使得
,使得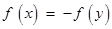
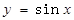 ;
;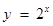 ;③
;③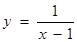 ;④
;④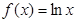 , 则其中“Ω函数”共有( )
, 则其中“Ω函数”共有( )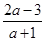 ,则实数a的取值范围是________.
,则实数a的取值范围是________.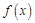 是定义在
是定义在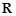 上的奇函数,当
上的奇函数,当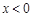 时,
时,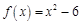 ,则
,则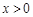 时,
时,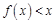 的解集为________.
的解集为________.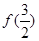 =
=