题目内容
18.已知定义在R上的奇函数f(x)的周期为4,其图象关于直线x=1对称,且当x∈(2,3]时,f(x)=-(x-2)(x-4),则f(sin$\frac{1}{2}$),f(sin1),f(cos2)的大小关系为( )| A. | f(cos2)>f(sin1)>f(sin$\frac{1}{2}$) | B. | f(cos2)>f(sin$\frac{1}{2}$)>f(sin1) | ||
| C. | f(sin$\frac{1}{2}$)>f(cos2)>f(sin1) | D. | f(sin1)>f(sin$\frac{1}{2}$)>f(cos2) |
分析 根据函数的对称性和函数的周期性,画出函数的图象,从而得到函数的单调性,进而求出函数值的大小.
解答 解:由题意得函数f(x)的图象关于直线x=1对称,
另外函数f(x)的周期为4,又当x∈(2,3]时,
f(x)=-(x-2)(x-4),
∴可以画出函数f(x)的图象,如图示: ,
,
可知函数f(x)在[-1,1]上单调递减,
又-1<cos2<0<sin$\frac{1}{2}$<sin1<1,
∴f(cos2)>f(sin$\frac{1}{2}$)>f(sin1),
故选:B.
点评 本题考查了函数的周期性、奇偶性,考查数形结合思想,是一道基础题.

练习册系列答案
相关题目
8.过点P(2,3),并且在两轴上的截距相等的直线方程是( )
| A. | x+y-5=0 | B. | 3x-2y=0 | ||
| C. | x+y-5=0或3x-2y=0 | D. | x-y+1=0或3x-2y=0 |
13.已知集合A={x|(x+1)(4-x)<0},集合B={y|y=2sin3x},则A∩B=( )
| A. | (-1,2] | B. | ( 2,4 ) | C. | [-2,-1 ) | D. | [-2,2] |
7.若第一象限的点(a,b)关于直线x+y-2=0的对称点在直线2x+y+3=0上,则$\frac{1}{a}+\frac{8}{b}$的最小值是( )
| A. | 1 | B. | 3 | C. | $\frac{25}{9}$ | D. | $\frac{17}{9}$ |
8. 已知函数f(x)=sinx?cosx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$.
已知函数f(x)=sinx?cosx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$.
(Ⅰ)化简函数f(x),并用“五点法”画出函数f(x)在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);
(Ⅱ)当x∈[0,$\frac{π}{2}$]时,求函数f(x)的最大值和最小值及相应的x的值.
 已知函数f(x)=sinx?cosx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$.
已知函数f(x)=sinx?cosx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$.(Ⅰ)化简函数f(x),并用“五点法”画出函数f(x)在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);
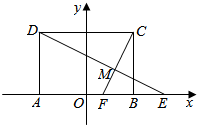 在矩形中ABCD中,AB=4,BC=2$\sqrt{3}$,M为动点,DM、CM的延长线与AB(或其延长线)分别交于点E、F,若$\overrightarrow{AE}$•$\overrightarrow{BF}$+$\overrightarrow{EF}$2=0.
在矩形中ABCD中,AB=4,BC=2$\sqrt{3}$,M为动点,DM、CM的延长线与AB(或其延长线)分别交于点E、F,若$\overrightarrow{AE}$•$\overrightarrow{BF}$+$\overrightarrow{EF}$2=0. 如图:平面直角坐标系中p(x,y)(y≠0)为一动点,A(-1,0),B(2,0)∠PBA=2∠PAB.
如图:平面直角坐标系中p(x,y)(y≠0)为一动点,A(-1,0),B(2,0)∠PBA=2∠PAB.