题目内容
10. 如图:平面直角坐标系中p(x,y)(y≠0)为一动点,A(-1,0),B(2,0)∠PBA=2∠PAB.
如图:平面直角坐标系中p(x,y)(y≠0)为一动点,A(-1,0),B(2,0)∠PBA=2∠PAB.(1)求动点P轨迹E的方程;
(2)过E上任意一P(x0,y0)向(x+1)2+y2=1作两条切线PF、PR,且PF、PR交y轴于M、N,求MN长度的取值范围.
分析 (1)由题意可得tan∠PBA=−yx−2−yx−2,tan∠PAB=yx+1yx+1,再根据tan∠PBA=tan2∠PAB=2tan∠PAB1−tan2∠PAB2tan∠PAB1−tan2∠PAB,化简可得点P的轨迹方程.
(2)设PF斜率为k1,PR斜率为k2,求得PF和PR的方程,可得|MN|=(k1-k2)x0|,再根据直线和圆相切的性质,k1、k2为 |y0−k(x0+1)|√k2+1=1的两个实数解,即(x02+2x0)k2-2y0(x0+1)k+y02-1=0,利用韦达定理可得k1+k2 和k1•k2,可得|MN|2=4[y02+x02+2x0](x0+2)2=4[4x02+2x0−3](x0+2)2,再利用导数判断它的单调性,由单调性求出|MN|的范围.
解答 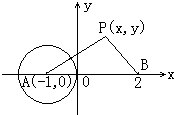 解:(1)由题意可得tan∠PBA=-KPB=−yx−2,tan∠PAB=KPA=yx+1,
解:(1)由题意可得tan∠PBA=-KPB=−yx−2,tan∠PAB=KPA=yx+1,
再根据∠PBA=2∠PAB,可得tan∠PBA=tan2∠PAB=2tan∠PAB1−tan2∠PAB,
即 −yx−2=2yx+11−(yx+1)2,化简可得 3x2-y2=3,即 x2-y23=1 (x>1).
(2)设PF斜率为k1,PR斜率为k2,
则PF:y-y0=k1(x-x0),PR:y-y0=k2(x-x0),
令x=0,可得yM=y0-k1x0,yN=y0-k2x0,∴|MN|=(k1-k2)x0|,
由PF和圆相切得:|−k1+y0−k1x0|√k12+1=1,PR和圆相切得:|−k2+y0−k2x0|√k22+1=1,
故:k1、k2为 |y0−k(x0+1)|√k2+1=1的两个实数解,
故有:(x02+2x0)k2-2y0(x0+1)k+y02-1=0,利用韦达定理可得k1+k2=2y0(x0+1)x02+2x0,k1•k2=y02−1x02+2x0.
|MN|2=x02[(k1+k2)2-4k1•k2]=x02[(k1+k2)2-4k1•k2]=4[y02+x02+2x0](x0+2)2,
又∵x02-y023=1,∴|MN|2=4[4x02+2x0−3](x0+2)2,
设g(x0)=4[4x02+2x0−3](x0+2)2,则g′(x0)=8(7x0+5)(x0+2)3 (x0>1),故g(x)在(1,+∞)上是增函数.
当x0趋于1时,g(x0)趋于43;当x0趋于+∞时,g(x0)趋于16,故|MN|2∈(43,16),
故|MN|的范围为(2√33,4).
点评 本题主要考查直线的斜率公式,求动点的轨迹方程,直线和圆锥曲线的位置关系,利用导数研究函数的单调性,属于难题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 183 | B. | 132 | C. | 528 | D. | 732 |
| A. | f(cos2)>f(sin1)>f(sin12) | B. | f(cos2)>f(sin12)>f(sin1) | ||
| C. | f(sin12)>f(cos2)>f(sin1) | D. | f(sin1)>f(sin12)>f(cos2) |
| A. |  | B. |  | C. |  | D. |  |
