题目内容
6．已知函数f（x）=$\frac{1}{2}$x2-2alnx+（a-2）x，a∈R．（1）当a=1时，求函数f（x）图象在点（1，f（1））处的切线方程；
（2）当a＜0时，讨论函数f（x）的单调性．
分析 先求出函数的导数（1）将a=1代入，求出f′（1）的值，从而求出切线方程；
（2）通过讨论a的范围，求出f′（x）的符号，从而得到函数的单调性．
解答 解 f′（x）=x-$\frac{2a}{x}$+a-2=$\frac{（x-2）（x+a）}{x}$，（x＞0），
（1）当a=1时，f′（x）=$\frac{（x-2）（x+1）}{x}$，f′（1）=-2，
∴所求的切线方程为y-f（1）=-2（x-1），即4x+2y-3=0．
（2）①当-a=2，即a=-2时，f′（x）=$\frac{{（x-2）}^{2}}{x}$≥0，f（x）在（0，+∞）上单调递增；
②当-a＜2，即-2＜a＜0时，∵0＜x＜-a或x＞2时，f′（x）＞0；-a＜x＜2时，f′（x）＜0，
f（x）在（0，-a），（2，+∞）上单调递增，在（-a，2）上单调递减；
③当-a＞2，即a＜-2时，∵0＜x＜2或x＞-a时，f′（x）＞0；
2＜x＜-a时，f′（x）＜0，f（x）在（0，2），（-a，+∞）上单调递增，在（2，-a）上单调递减，
综上a=-2时，f（x）在（0，+∞）上单调递增．
-2＜a＜0时，f（x）在（0，-a），（2，+∞）上单调递增，在（-a，2）上单调递减，
a＜-2时，f（x）在（0，2），（-a，+∞）上单调递增，在（2，-a）上单调递减．
点评 本题考查了曲线的切线方程问题，考查函数的单调性问题，考查导数的应用，是一道中档题．
练习册系列答案
相关题目
17．直线y=a与椭圆$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1恒有两个不同交点，则a的取值范围是（ ）
| A． | （-$\sqrt{3}$，$\sqrt{3}$） | B． | （-3，3） | C． | （-2，2） | D． | （-4，4） |
14．（x-$\frac{2}{\sqrt{x}}$）6的展开式中的常数项为（ ）
| A． | 240 | B． | -240 | C． | 72 | D． | -72 |
1．数列{an}满足：a1=1，且对每个n∈N*，an，an+1是方程x2+3nx+bn=0的两根，则bn的前6项的和的4倍为（ ）
| A． | 183 | B． | 132 | C． | 528 | D． | 732 |
18．已知定义在R上的奇函数f（x）的周期为4，其图象关于直线x=1对称，且当x∈（2，3]时，f（x）=-（x-2）（x-4），则f（sin$\frac{1}{2}$），f（sin1），f（cos2）的大小关系为（ ）
| A． | f（cos2）＞f（sin1）＞f（sin$\frac{1}{2}$） | B． | f（cos2）＞f（sin$\frac{1}{2}$）＞f（sin1） | ||
| C． | f（sin$\frac{1}{2}$）＞f（cos2）＞f（sin1） | D． | f（sin1）＞f（sin$\frac{1}{2}$）＞f（cos2） |
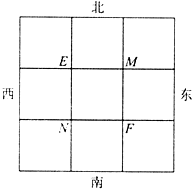已知甲、乙两人分别位于图中的M、N两点，每隔1分钟，甲、乙两人分别向东南西北四个方向的其中一个方向行走1格，且甲向四个方向行走的概率是相等的，乙向东、向西行走的概率都是$\frac{1}{3}$，向北行走的概率是$\frac{1}{4}$，甲、乙分别向某个方向行走的事件记为A、B．