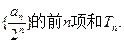题目内容
已知定义域为R的二次函数f(x)的最小值为0,且有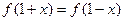 ,直线
,直线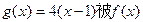 图象截得的弦长为
图象截得的弦长为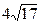 ,数列
,数列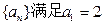 ,
,
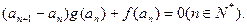
⑴ 求函数f(x)的解析式;
⑵ 求数列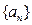 的通项公式;
的通项公式;
⑶ 设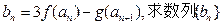 的最值及相应的n.
的最值及相应的n.
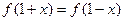 ,直线
,直线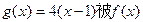 图象截得的弦长为
图象截得的弦长为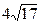 ,数列
,数列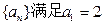 ,
,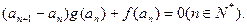
⑴ 求函数f(x)的解析式;
⑵ 求数列
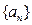 的通项公式;
的通项公式;⑶ 设
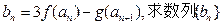 的最值及相应的n.
的最值及相应的n.(1)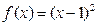 (2)
(2)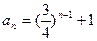
(3)当n = 1时,x=1,bn最大值为0
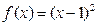 (2)
(2)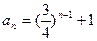
(3)当n = 1时,x=1,bn最大值为0
(1)因为二次函数f(x)有最小值为0,所以a>0,又因为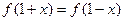 , 所以对称轴为x=1,所以设
, 所以对称轴为x=1,所以设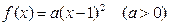 ……① 又
……① 又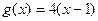 …②
…②
联立①②组成方程组解得两图象的交点坐标为(1,0),(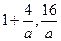 ),依题意得
),依题意得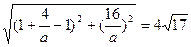 ,因为a>0,所以解得a=1,所以
,因为a>0,所以解得a=1,所以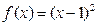
⑵由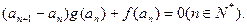 ,
,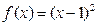 ,
,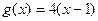
得,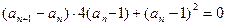 ,因为
,因为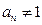 ,所以
,所以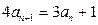 ,所以
,所以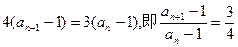 ,又
,又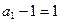 ,所以数列{
,所以数列{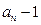 }是以1为首项,
}是以1为首项,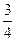 为公比的等比数列,所以
为公比的等比数列,所以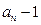 =1
=1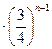 ,所以
,所以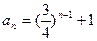
(3)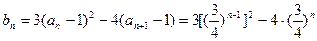
令
则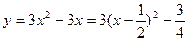
因为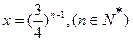
所以当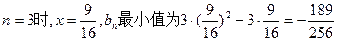
当n = 1时,x=1,bn最大值为0
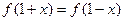 , 所以对称轴为x=1,所以设
, 所以对称轴为x=1,所以设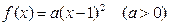 ……① 又
……① 又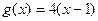 …②
…②联立①②组成方程组解得两图象的交点坐标为(1,0),(
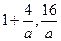 ),依题意得
),依题意得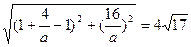 ,因为a>0,所以解得a=1,所以
,因为a>0,所以解得a=1,所以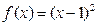
⑵由
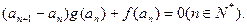 ,
,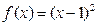 ,
,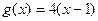
得,
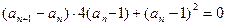 ,因为
,因为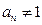 ,所以
,所以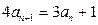 ,所以
,所以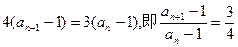 ,又
,又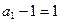 ,所以数列{
,所以数列{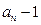 }是以1为首项,
}是以1为首项,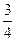 为公比的等比数列,所以
为公比的等比数列,所以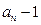 =1
=1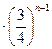 ,所以
,所以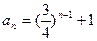
(3)
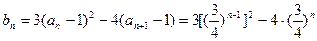
令

则
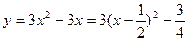
因为
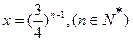
所以当
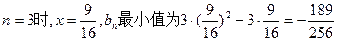
当n = 1时,x=1,bn最大值为0

练习册系列答案
相关题目
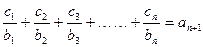 ,
,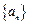 是等差数列,从
是等差数列,从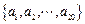 中任取3个不同的数,使这3个数仍成等差数列,则这样不同的等差数列的个数最多有( )
中任取3个不同的数,使这3个数仍成等差数列,则这样不同的等差数列的个数最多有( )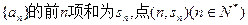 在函数
在函数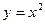 的图象上,数列
的图象上,数列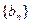 满足
满足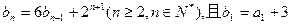 (1)求数列
(1)求数列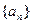 的通项公式;(2)证明列数
的通项公式;(2)证明列数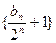 是等比数列,并求数列
是等比数列,并求数列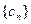 满足对任意的
满足对任意的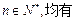
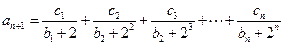 成立,
成立,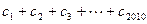 的值。
的值。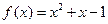 ,
,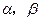 是方程
是方程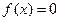 的两个根
的两个根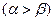 ,
,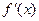 是
是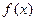 的导数.设
的导数.设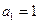 ,
,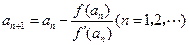 .
.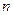 有
有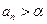 ,记
,记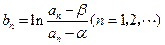 .求数列
.求数列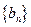 的前
的前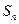 .
.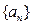 的前n项和
的前n项和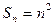 ,
, 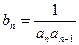 ,求数列
,求数列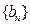 的前n项和
的前n项和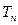 .
.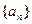 的前
的前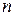 项的和为
项的和为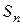 ,且
,且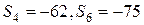 ,求:
,求: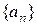 的通项公式
的通项公式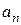 及前
及前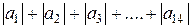
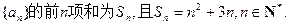
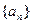 的通项公式; (II)求数列
的通项公式; (II)求数列