题目内容
(本小题12分)
已知动点P到定点A(0,1)的距离比它到定直线y = -2的距离小1.
(I)求动点P的轨迹C的方程;
(II)已知点Q为直线y= -1上的动点,过点q作曲线C的两条切线,切点分别为M,N,求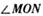 的取值范围.(其中O为坐标原点)
的取值范围.(其中O为坐标原点)
已知动点P到定点A(0,1)的距离比它到定直线y = -2的距离小1.
(I)求动点P的轨迹C的方程;
(II)已知点Q为直线y= -1上的动点,过点q作曲线C的两条切线,切点分别为M,N,求
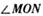 的取值范围.(其中O为坐标原点)
的取值范围.(其中O为坐标原点)解:(Ⅰ)由动点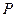 到定点
到定点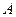
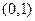 的距离比到定直线
的距离比到定直线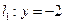 的距离小
的距离小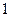 ,可知
,可知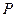 到定点
到定点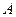
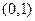 的距离等于到直线
的距离等于到直线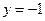 的距离,由抛物线定义可知动点
的距离,由抛物线定义可知动点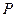 的轨迹方程为
的轨迹方程为 .………………………………4分
.………………………………4分
(Ⅱ)法一由题意知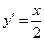 ,设
,设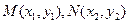 ,
, ,
,
则切线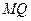 :
: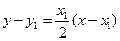 ,
,
切线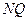 :
: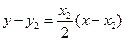 ,……………………6分
,……………………6分
又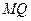 ,
,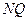 交于
交于 ,故
,故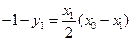 ,
,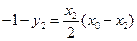 ,又
,又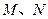 在
在 上,
上,
则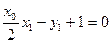 ,
,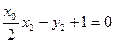 .
.
可得直线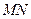 :
: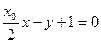 ,又
,又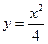 ,可得
,可得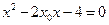 .
.
由韦达定理可知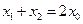 ,
,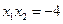 , 不妨设
, 不妨设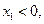 ……………………8分
……………………8分
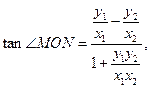 由
由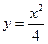
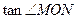
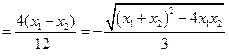
=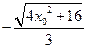
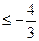 ,……………………………10分
,……………………………10分
所以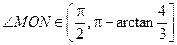 .…………………………12分
.…………………………12分
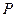 到定点
到定点
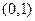 的距离比到定直线
的距离比到定直线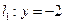 的距离小
的距离小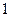 ,可知
,可知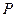 到定点
到定点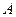
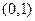 的距离等于到直线
的距离等于到直线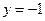 的距离,由抛物线定义可知动点
的距离,由抛物线定义可知动点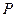 的轨迹方程为
的轨迹方程为 .………………………………4分
.………………………………4分(Ⅱ)法一由题意知
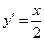 ,设
,设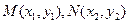 ,
, ,
,则切线
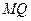 :
: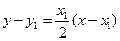 ,
,切线
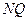 :
: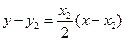 ,……………………6分
,……………………6分又
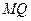 ,
,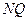 交于
交于 ,故
,故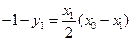 ,
,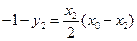 ,又
,又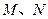 在
在 上,
上,则
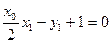 ,
,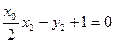 .
.可得直线
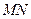 :
: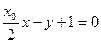 ,又
,又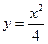 ,可得
,可得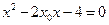 .
.由韦达定理可知
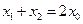 ,
,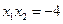 , 不妨设
, 不妨设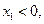 ……………………8分
……………………8分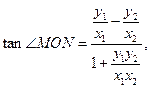 由
由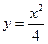
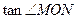
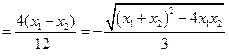
=
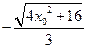
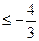 ,……………………………10分
,……………………………10分所以
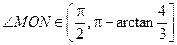 .…………………………12分
.…………………………12分略

练习册系列答案
相关题目
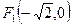 和
和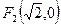 ,点
,点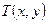 满足
满足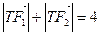
 ,
,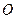 为直角坐标原点,
为直角坐标原点,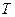 的轨迹方程
的轨迹方程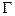 ; (6分)
; (6分)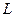 与轨迹方程
与轨迹方程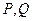 两点,三条直线
两点,三条直线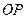 ,
,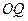 ,
,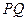 的斜率分别是
的斜率分别是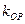 、
、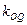 、
、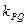 ,
,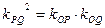 ,求
,求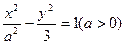 的两个焦点分别为
的两个焦点分别为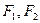 ,离心率为
,离心率为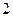 .
.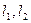 的方程;
的方程;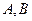 分别为
分别为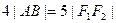 ,求线段
,求线段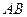 的中点
的中点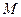 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.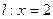 ,设动点P到直线
,设动点P到直线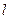 的距离为
的距离为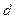 ,已知
,已知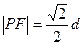 ,且
,且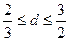 .
.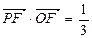 ,求向量
,求向量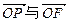 的夹
的夹 角;
角; ,点M满足
,点M满足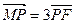 ,且线段MG的垂直平分线经过点P,求
,且线段MG的垂直平分线经过点P,求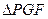 的面积
的面积 足条件
足条件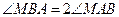 ,求动
,求动 点M的轨迹方程并指出轨迹是什么图形
点M的轨迹方程并指出轨迹是什么图形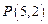 、
、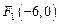 、
、 .
.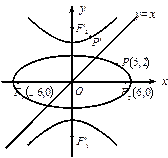
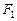 、
、 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;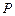 、
、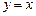 的对称点分别为
的对称点分别为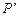 、
、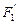 、
、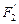 ,求以
,求以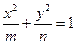 满足条件:
满足条件: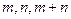 成等差数列,则椭圆离心率为
成等差数列,则椭圆离心率为 ( )
( )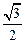
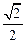

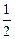
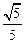

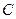 上的动点
上的动点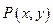 满足到点
满足到点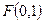 的距离比到直线
的距离比到直线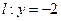 的距离小
的距离小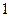 .
. 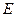 在直线
在直线 上,过点
上,过点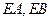 ,切点为
,切点为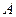 、
、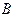 .
.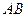 恒过一定点,并求出该定点的坐标;
恒过一定点,并求出该定点的坐标;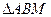 为等边三角形(
为等边三角形(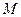 点也在直线
点也在直线