题目内容
6.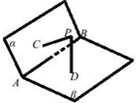 如图,已知二面角α-AB-β的大小为120°,PC⊥α,PD⊥β,C、D是垂足,C、D不在直线AB上,PC=PD=$\sqrt{3}$,有如下命题:
如图,已知二面角α-AB-β的大小为120°,PC⊥α,PD⊥β,C、D是垂足,C、D不在直线AB上,PC=PD=$\sqrt{3}$,有如下命题:①直线AB与直线CD是异面直线;
②直线AB与直线CD垂直;
③∠CPD=60°;
④点P到直线AB的距离是2,
其中正确命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 如图所示,设平面PCD与AB相交于点Q,连接CQ,QD.由于PC⊥α,PD⊥β,α∩β=AB.可得PC⊥AB,PD⊥AB,AB⊥CQ,AB⊥QD,于是∠CQD是二面角α-AB-β的平面角,大小为120°.即可判断出正误.
解答 解:如图所示,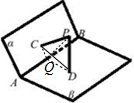
设平面PCD与AB相交于点Q,连接CQ,QD.
∵PC⊥α,PD⊥β,α∩β=AB.
∴PC⊥AB,PD⊥AB,
∴AB⊥平面PCQD.
∴AB⊥CQ,AB⊥QD,
∴∠CQD是二面角α-AB-β的平面角,大小为120°.
因此:直线AB与直线CD是异面直线;直线AB与直线CD垂直;∠CPD=60°;由PC=PD=$\sqrt{3}$,可得点P到直线AB的距离是2.
其中正确命题的个数是4.
故选:D.
点评 本题考查了空间位置关系及其空间角,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
16.设X~B(10,0.8)则k=( )时,P(x=k)最大.
| A. | 8 | B. | 9 | C. | 8或9 | D. | 7或8 |
14.4×5×6×…×(n-1)×n=( )
| A. | Cn4 | B. | n!-3! | C. | Ann-3 | D. | Cnn-3 |
16.若复数z满足(1-i)z=1+i,则|z+i|=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |