题目内容
18.已知点A的坐标(x,y)满足不等式$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+2y≤6}\\{3x+y≤12}\end{array}\right.$,则|x-y|的取值范围是[0,4].分析 z=x-y,作出不等式组对应的平面区域,利用z的几何意义进行求解即可.
解答  解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
设z=x-y,得y=x-z表示,斜率为1纵截距为-z的一组平行直线,
平移直线y=x-z,当直线y=x-z经过点C(4,0)时,直线y=x-z的截距最小,此时z最大,为z=4,
当直线经过点A(0,3)时,此时直线y=x-z截距最大,z最小.此时z=0-3=-3,
则-3≤z≤4,
则0≤|z|≤4,
即|x-y|的取值范围是[0,4],
故答案为:[0,4].
点评 本题主要考查线性规划的基本应用,利用z的几何意义是解决线性规划问题的关键,注意利用数形结合来解决.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
9.甲、乙两位同学在几次数学测验中,各自的平均成绩都是88分,甲的方差为0.61,乙的方差为0.72,则( )
| A. | 甲的成绩比乙的成绩稳定 | B. | 乙的成绩比甲的成绩好 | ||
| C. | 甲、乙的成绩一样 | D. | 甲、乙的成绩无法比较 |
6.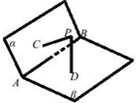 如图,已知二面角α-AB-β的大小为120°,PC⊥α,PD⊥β,C、D是垂足,C、D不在直线AB上,PC=PD=$\sqrt{3}$,有如下命题:
如图,已知二面角α-AB-β的大小为120°,PC⊥α,PD⊥β,C、D是垂足,C、D不在直线AB上,PC=PD=$\sqrt{3}$,有如下命题:
①直线AB与直线CD是异面直线;
②直线AB与直线CD垂直;
③∠CPD=60°;
④点P到直线AB的距离是2,
其中正确命题的个数是( )
 如图,已知二面角α-AB-β的大小为120°,PC⊥α,PD⊥β,C、D是垂足,C、D不在直线AB上,PC=PD=$\sqrt{3}$,有如下命题:
如图,已知二面角α-AB-β的大小为120°,PC⊥α,PD⊥β,C、D是垂足,C、D不在直线AB上,PC=PD=$\sqrt{3}$,有如下命题:①直线AB与直线CD是异面直线;
②直线AB与直线CD垂直;
③∠CPD=60°;
④点P到直线AB的距离是2,
其中正确命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
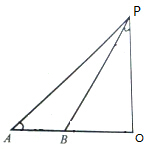 如图,塔PO与地平线AO垂直,在A点测得塔顶P的仰角∠PAO=45°,沿AO方向前进至B点,测得仰角∠PBO=60°,A,B相距44m,求塔高PO(精确到0.1m).
如图,塔PO与地平线AO垂直,在A点测得塔顶P的仰角∠PAO=45°,沿AO方向前进至B点,测得仰角∠PBO=60°,A,B相距44m,求塔高PO(精确到0.1m).