题目内容
16．若复数z满足（1-i）z=1+i，则|z+i|=（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 根据复数的四则运算先求出复数z，再计算复数z+i的模长．
解答 解：∵（1-i）z=1+i，
∴z=$\frac{1+i}{1-i}$=$\frac{{（1+i）}^{2}}{1{-i}^{2}}$=i，
∴|z+i|=|2i|=2．
故选：C．
点评 本题考查了复数的四则运算与求复数模长的应用问题，是基础题目．
练习册系列答案
相关题目
6．
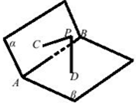如图，已知二面角α-AB-β的大小为120°，PC⊥α，PD⊥β，C、D是垂足，C、D不在直线AB上，PC=PD=$\sqrt{3}$，有如下命题：
①直线AB与直线CD是异面直线；
②直线AB与直线CD垂直；
③∠CPD=60°；
④点P到直线AB的距离是2，
其中正确命题的个数是（ ）
如图，已知二面角α-AB-β的大小为120°，PC⊥α，PD⊥β，C、D是垂足，C、D不在直线AB上，PC=PD=$\sqrt{3}$，有如下命题：①直线AB与直线CD是异面直线；
②直线AB与直线CD垂直；
③∠CPD=60°；
④点P到直线AB的距离是2，
其中正确命题的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
11．某城市随机抽取一年（365天）内100天的空气质量指数API的监测数据，统计结果如下：
（1）若某企业每天由空气污染造成的经济损失S（单位：元）与空气质量指数API（记为ω）的关系式为：
S=$\left\{\begin{array}{l}0，0≤ω≤100\\ 4ω-400，100＜ω≤300\\ 2000，ω＞300.\end{array}\right.$试估计在本年内随机抽取一天，该天经济损失S大于200元且不超过600元的概率；
（2）若以上表统计的频率作为概率，求该城市某三天中恰有一天空气质量为轻度污染的概率．（假定这三天中空气质量互不影响）
| API | [0，50] | （50，100] | （100，150] | （150，200] | （200，250] | （250，300] | ＞300 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
S=$\left\{\begin{array}{l}0，0≤ω≤100\\ 4ω-400，100＜ω≤300\\ 2000，ω＞300.\end{array}\right.$试估计在本年内随机抽取一天，该天经济损失S大于200元且不超过600元的概率；
（2）若以上表统计的频率作为概率，求该城市某三天中恰有一天空气质量为轻度污染的概率．（假定这三天中空气质量互不影响）
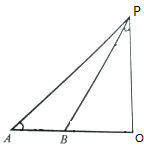如图，塔PO与地平线AO垂直，在A点测得塔顶P的仰角∠PAO=45°，沿AO方向前进至B点，测得仰角∠PBO=60°，A，B相距44m，求塔高PO（精确到0.1m）．