题目内容
【题目】已知函数f(x)= 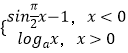 (a>0且a≠1)的图象上关于y轴对称的点至少有3对,则实数a的范围是( )
(a>0且a≠1)的图象上关于y轴对称的点至少有3对,则实数a的范围是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.( ![]() ,1)
,1)
D.(0, ![]() )
)
【答案】A
【解析】解:若x>0,则﹣x<0,∵x<0时,f(x)=sin( ![]() x)﹣1,
x)﹣1,
∴f(﹣x)=sin(﹣ ![]() x)﹣1=﹣sin(
x)﹣1=﹣sin( ![]() x)﹣1,
x)﹣1,
则若f(x)=sin( ![]() x)﹣1,(x<0)关于y轴对称,
x)﹣1,(x<0)关于y轴对称,
则f(﹣x)=﹣sin( ![]() x)﹣1=f(x),即y=﹣sin(
x)﹣1=f(x),即y=﹣sin( ![]() x)﹣1,x>0,
x)﹣1,x>0,
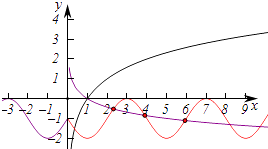
设g(x)=﹣sin( ![]() x)﹣1,x>0,作出函数g(x)的图象,
x)﹣1,x>0,作出函数g(x)的图象,
要使y=﹣sin( ![]() x)﹣1,x>0与f(x)=logax,x>0的图象至少有3个交点,如图,
x)﹣1,x>0与f(x)=logax,x>0的图象至少有3个交点,如图,
则0<a<1且满足g(5)<f(5),
即﹣2<loga5,即loga5>logaa﹣2,则5< ![]() ,解得0<a<
,解得0<a< ![]() ,
,
故选:A.
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.

练习册系列答案
相关题目