题目内容
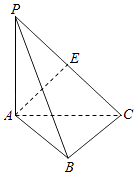
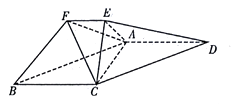
【题目】在如图所示的几何体中,平面 ![]() 平面
平面 ![]() ,四边形
,四边形 ![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)求证: ![]() 平面
平面 ![]() ;
;
(2)求 ![]() 到平面
到平面 ![]() 的距离;
的距离;
(3)求三棱锥 ![]() 的体积.
的体积.
【答案】
(1)证明:∵平面 ![]() 平面
平面 ![]() ,且平面
,且平面 ![]() 平面
平面 ![]() ,
,
又 ![]() 平面
平面 ![]() ,
, ![]() ,
,
∴ ![]() 平面
平面 ![]() ,
,
而 ![]() 平面
平面 ![]() ,∴
,∴ ![]() ,
,
∵ ![]() ,
, ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
,
又 ![]() ,∴
,∴ ![]() 平面
平面 ![]()
(2)解:设 ![]() 的中点为
的中点为 ![]() ,连接
,连接 ![]() ,
,
∵ ![]() ,∴
,∴ ![]() .
.
∵平面 ![]() 平面
平面 ![]() ,且平面
,且平面 ![]() 平面
平面 ![]() ,
,
∴ ![]() 平面
平面 ![]() ,
,
∵ ![]() ,
, ![]() 平面
平面 ![]() ,
,
所以点 ![]() 到平面
到平面 ![]() 的距离就等于点
的距离就等于点 ![]() 到平面
到平面 ![]() 的距离,
的距离,
即点 ![]() 到平面
到平面 ![]() 的距离为
的距离为 ![]()
(3)解:∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,即三棱锥
,即三棱锥 ![]() 的体积为
的体积为 ![]() .
.
【解析】(1)首先根据面面垂直的性质定理即可得证 B C ⊥ 平面 A E C进而得出B C ⊥ A E,再利用勾股定理的逆定理得出A E ⊥ E C 结合线面垂直的判定定理进而得到 A E ⊥ 平面 B C E F。(2)根据题意作出辅助线结合题意利用面面垂直的性质定理可得出E G ⊥ 平面 A B C D,再结合平行性质转化垂直关系可得点 F 到平面 A B C D 的距离就等于点 E 到平面 A B C D 的距离,由已知的长度关系代入数值求出结果即可。(3)利用(1)(2)的结论把数值代入到三棱锥的体积公式求出结果即可。

【题目】性格色彩学创始人乐嘉是江苏电视台当红节目“非诚勿扰”的特约嘉宾,他的点评视角独特,语言犀利,给观众留下了深刻的印象,某报社为了了解观众对乐嘉的喜爱程度,随机调查了观看了该节目的140名观众,得到如下的列联表:(单位:名)
男 | 女 | 总计 | |
喜爱 | 40 | 60 | 100 |
不喜爱 | 20 | 20 | 40 |
总计 | 60 | 80 | 140 |
(Ⅰ)从这60名男观众中按对乐嘉是否喜爱采取分层抽样,抽取一个容量为6的样本,问样本中喜爱与不喜爱的观众各有多少名?
(Ⅱ)根据以上列联表,问能否在犯错误的概率不超过0.025%的前提下认为观众性别与喜爱乐嘉有关.(精确到0.001)
(Ⅲ)从(Ⅰ)中的6名男性观众中随机选取两名作跟踪调查,求选到的两名观众都喜爱乐嘉的概率.
附:
p(k2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k0 | 2.705 | 3.841 | 5.024 | 6.635 | 7.879 |
k2= ![]() .
.