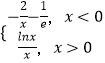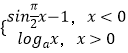题目内容
【题目】已知函数 ![]() 是奇函数且当
是奇函数且当 ![]() 时是减函数,若
时是减函数,若 ![]() ,则函数
,则函数 ![]() 的零点共有( )
的零点共有( )
A.4个
B.5个
C.6个
D.7个
【答案】D
【解析】根据题意,函数y=f(x)是定义域为R的奇函数,则f(0)=0,
当x∈(0,+∞)时是减函数,且f(1)=0,则函数在(0,+∞)上只有一个零点,
若函数y=f(x)是奇函数且当x∈(0,+∞)时是减函数,则f(x)在(-∞,0)为减函数,
又由f(1)=0,则f(-1)=-f(1)=0,则函数在(-∞,0)上只有一个零点,
故函数y=f(x)共有3个零点,依次为-1、0、1,
对于函数 ![]() ,
,
当 ![]() 时,解得
时,解得 ![]() ,
,
当 ![]() 时,解得
时,解得 ![]() 或x=0,
或x=0,
当 ![]() 时,解得
时,解得 ![]() 或
或 ![]() . 故函数
. 故函数 ![]() 的零点共有7个.
的零点共有7个.
所以答案是:D.
【考点精析】掌握函数单调性的性质和函数奇偶性的性质是解答本题的根本,需要知道函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集;在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.

练习册系列答案
相关题目