题目内容
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知sinB(tanA+tanC)=tanAtanC.
(1)求证:a,b,c成等比数列;
(2)若a=1,c=2,求△ABC的面积S.
【答案】
(1)证明:∵sinB(tanA+tanC)=tanAtanC
∴sinB( ![]() )=
)= ![]()
∴sinB ![]() =
= ![]()
∴sinB(sinAcosC+sinCcosA)=sinAsinc
∴sinBsin(A+C)=sinAsinC,
∵A+B+C=π
∴sin(A+C)=sinB
即sin2B=sinAsinC,
由正弦定理可得:b2=ac,
所以a,b,c成等比数列.
(2)解:若a=1,c=2,则b2=ac=2,
∴ ![]() ,
,
∵0<B<π
∴sinB= ![]()
∴△ABC的面积 ![]()
【解析】(1)由已知,利用三角函数的切化弦的原则可得,sinB(sinAcosC+sinCcosA)=sinAsinC,利用两角和的正弦公式及三角形的内角和公式代入可得sin2B=sinAsinC,由正弦定理可证(2)由已知结合余弦定理可求cosB,利用同角平方关系可求sinB,代入三角形的面积公式S= ![]() 可求.
可求.
【考点精析】认真审题,首先需要了解等比数列的基本性质({an}为等比数列,则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列).

 期末集结号系列答案
期末集结号系列答案【题目】2015年12月,华中地区数城市空气污染指数“爆表”,此轮污染为2015年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)(I)利用(1)所求的回归方程,预测该市车流量为12万辆时![]() 的浓度;(II)规定:当一天内
的浓度;(II)规定:当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量不超过多少万辆?(结果以万辆为单位,保留整数)参考公式:回归直线的方程是
内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量不超过多少万辆?(结果以万辆为单位,保留整数)参考公式:回归直线的方程是![]() ,其中
,其中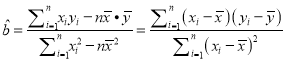 ,
, ![]() .
.