题目内容
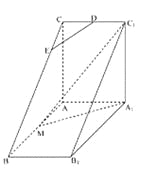
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是等腰三角形,
是等腰三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上一点.
上一点.
(I)若![]() 平面
平面![]() ,求
,求![]() ;
;
(II)平面![]() 将三棱柱
将三棱柱![]() 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(I)借助题设条件运用线面的位置关系求解;(II)借助题设运用体积割补的方法探求.
试题解析:
(I)取![]() 中点为
中点为![]() ,连接
,连接![]() ,
,![]() ,………………1分
,………………1分
∵![]() 分别
分别![]() ,
,![]() 为中点,
为中点,
∴![]() ,∴
,∴![]() 四点共面,………………3分
四点共面,………………3分
且平面![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() 是
是![]() 的中点,∴
的中点,∴![]() .………………6分
.………………6分
(II)因为三棱柱![]() 为直三棱柱,∴
为直三棱柱,∴![]() 平面
平面![]() ,
,
又![]() ,则
,则![]() 平面
平面![]() ,
,
设![]() ,又三角形
,又三角形![]() 是等腰三角形,所以
是等腰三角形,所以![]() .
.
如图,将几何体![]() 补成三棱柱
补成三棱柱![]() .
.
∴几何![]() 体的体积为:
体的体积为:
![]() .………………9分
.………………9分
又直三棱柱![]() 体积为:
体积为:![]() ,………………11分
,………………11分
故剩余的几何体棱台![]() 的体积为
的体积为![]() .
.
∴较小部分的体积与较大部分体积之比为:![]() .………………12分
.………………12分

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目